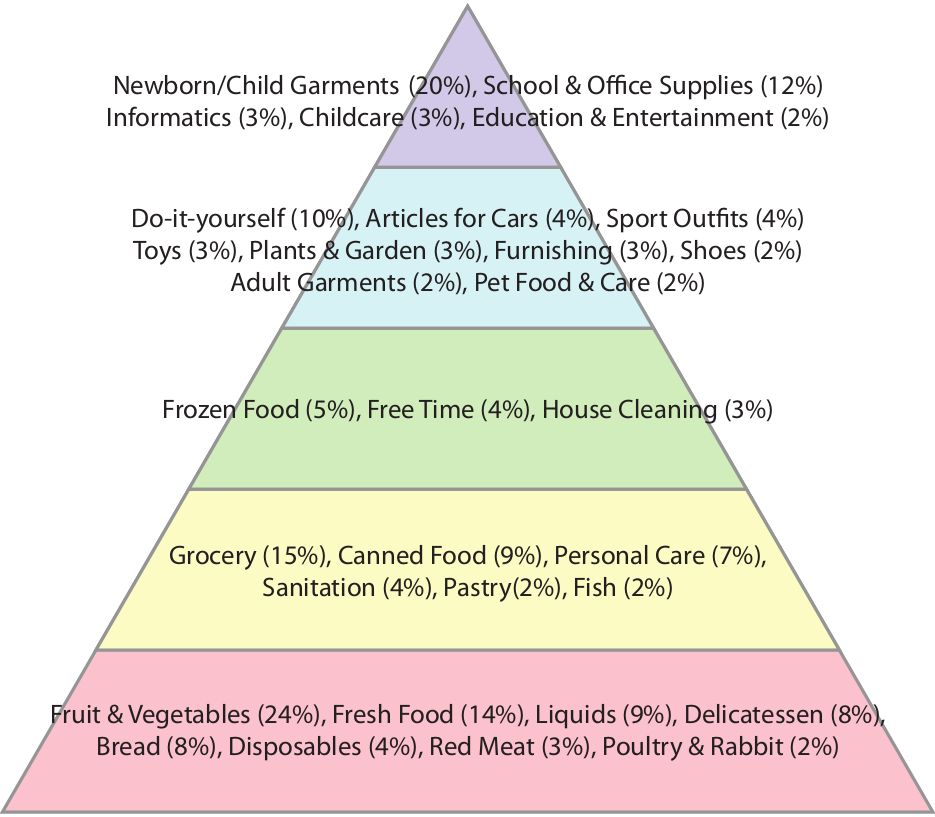
Evaluating Prosperity Beyond GDP
When reporting on economics, news outlets very often refer to what happens to the GDP. How is policy X going to affect our GDP? Is the national debt too high compared to GDP? How does my GDP compare to yours? The concept lurking behind those three letters is the Gross Domestic Product, the measure of the gross value added by all domestic producers in a country. In principle, the idea of using GDP to take the pulse of an economy isn’t bad: we count how much we can produce, and this is more or less how well we are doing. In practice, today I am jumping on the huge bandwagon of people who despise GDP for its meaningless, oversimplified and frankly suspicious nature. I will talk about a paper in which my co-authors and I propose to use a different measure to evaluate a country’s prosperity. The title is “Going Beyond GDP to Nowcast Well-Being Using Retail Market Data“, my co-authors are Riccardo Guidotti, Dino Pedreschi and Diego Pennacchioli, and the paper will be presented at the Winter edition of the Network Science Conference.
GDP is gross for several reasons. What Simon Kuznets said resonates strongly with me, as already in the 30s he was talking like a complexity scientist:
The valuable capacity of the human mind to simplify a complex situation in a compact characterization becomes dangerous when not controlled in terms of definitely stated criteria. With quantitative measurements especially, the definiteness of the result suggests, often misleadingly, a precision and simplicity in the outlines of the object measured. Measurements of national income are subject to this type of illusion and resulting abuse, especially since they deal with matters that are the center of conflict of opposing social groups where the effectiveness of an argument is often contingent upon oversimplification.
In short, GDP is an oversimplification, and as such it cannot capture something as complex as an economy, or the multifaceted needs of a society. In our paper, we focus on some of its specific aspects. Income inequality skews the richness distribution, so that GDP doesn’t describe how the majority of the population is doing. But more importantly, it is not possible to quantify well-being just with the number of dollars in someone’s pocket: she might have dreams, aspirations and sophisticated needs that bear little to no correlation with the status of her wallet. And even if GDP was a good measure, it’s very hard to calculate: it takes months to estimate it reliably. Nowcasting it would be great.
And so we tried to hack our way out of GDP. The measure we decided to use is the one of customer sophistication, that I presented several times in the past. In practice, the measure is a summary of the connectivity of a node in a bipartite network*. The bipartite network connects customers to the products they buy. The more variegated the set of products a customer buys, the more complex she is. Our idea was to create an aggregated version at the network level, and to see if this version was telling us something insightful. We could make a direct correlation with the national GDP of Italy, because the data we used to calculate it comes from around a half million customers from several Italian regions, which are representative of the country as a whole.
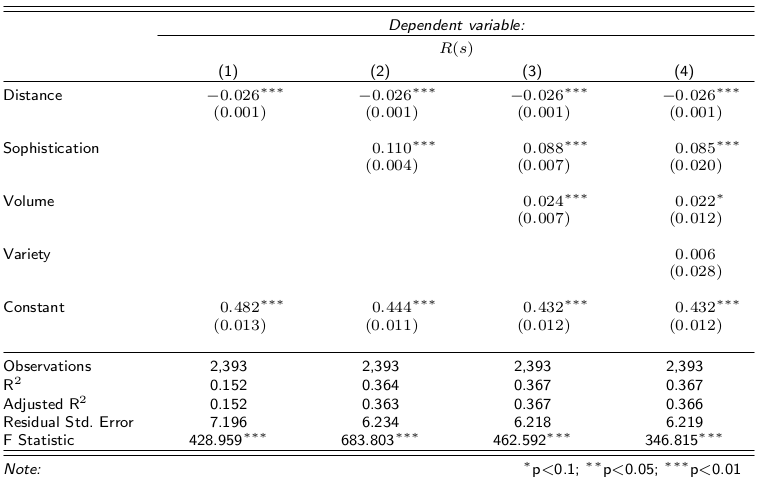
The argument we made goes as follows. GDP stinks, but it is not 100% bad, otherwise nobody would use it. Our sophistication is better, because it is connected to the average degree with which a person can satisfy her needs**. Income inequality does not affect it either, at least not in trivial ways as it does it with GDP. Therefore, if sophistication correlates with GDP it is a good measure of well-being: it captures part of GDP and adds something to it. Finally, if the correlation happens with some anticipated temporal shift it is even better, because GDP pundits can just use it as instantaneous nowcasting of GDP.
We were pleased when our expectations met reality. We tested several versions of the measure at several temporal shifts — both anticipating and following the GDP estimate released by the Italian National Statistic Institute (ISTAT). When we applied the statistical correction to control for the multiple hypothesis testing, the only surviving significant and robust estimate was our customer sophistication measure calculated with a temporal shift of -2, i.e. two quarters before the corresponding GDP estimate was released. Before popping our champagne bottles, let me write an open letter to the elephant in the room.
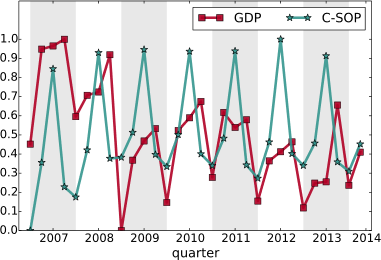
As you see from the above chart, there are some wild seasonal fluctuations. This is rather obvious, but controlling for them is not easy. There is a standard approach — the X-13-Arima method — which is more complicated than simply averaging out the fluctuations. It takes into account a parameter tuning procedure including information we simply do not have for our measure, besides requiring observation windows longer than what we have (2007-2014). It is well possible that our result could disappear. It is also possible that the way we calculated our sophistication index makes no sense economically: I am not an economist and I do not pretend for a moment that I can tell them how to do their job.
What we humbly report is a blip on the radar. It is that kind of thing that makes you think “Uh, that’s interesting, I wonder what it means”. I would like someone with a more solid skill set in economics to take a look at this sophistication measure and to do a proper stress-test with it. I’m completely fine with her coming back to tell me I’m a moron. But that’s the risk of doing research and to try out new things. I just think that it would be a waste not to give this promising insight a chance to shine.
* Even if hereafter I talk only about the final measure, it is important to remark that it is by no means a complete substitute of the analysis of the bipartite network. Meaning that I’m not simply advocating to substitute a number (GDP) for another (sophistication), rather to replace GDP with a fully-blown network analysis.
** Note that this is a revealed measure of sophistication as inferred by the products actually bought and postulating that each product satisfies one or a part of a “need”. If you feel that the quality of your life depends on you being able to bathe in the milk of a virgin unicorn, the measure will not take into account the misery of this tacit disappointment. Such are the perils of data mining.