Surprising Facts About Shortest Paths
Maybe it’s the new year, maybe it’s the fact that I haven’t published anything new recently, but today I wanted to take a look at my publication history. This, for a scientist, is something not unlike a time machine, bringing her back to an earlier age. What was I thinking in 2009? What sparked my interest and what were the tools further refined to get to the point where I am now? It’s usually a humbling (not to say embarrassing) operation, as past papers always look so awful – mine, at least. But small interesting bits can be found, like the one I retrieved today, about shortest paths in communication networks.
A shortest path in a network is the most efficient way to go from one node to another. You start from your origin and you choose to follow an edge to another node. Then you choose again an edge and so on until you get to your destination. When your choices are perfect and you used the minimum possible number of edges to follow, that’s a shortest path (it’s A shortest path and not THE shortest path because there might be alternative paths of the same length). Now, in creating this path, you obviously visited some nodes in between, unless your origin and destination are directly connected. Turns out that there are some nodes that are crossed by a lot of shortest paths, it’s a characteristic of real world networks. This is interesting, so scientists decided to create a measure called betweenness centrality. For each node, betweenness centrality is the share of all possible shortest paths in the network that pass through them.
Intuitively, these nodes are important. Think about a rail network, where the nodes are the train stations. High betweenness stations see a lot of trains passing through them. They are big and important to make connections run faster: if they didn’t exist every train would have to make detours and would take longer to bring you home. A good engineer would then craft rail networks in such a way to have these hubs and make her passengers happy. However, it turns out that this intuitive rule is not universally applicable. For example some communication networks aren’t willing to let this happen. Michele Berlingerio, Fosca Giannotti and I stumbled upon this interesting result while working on a paper titled Mining the Temporal Dimension of the Information Propagation.
We built two communication networks. One is corporate-based: it’s the web of emails exchanged across the Enron employee ecosystem. The email record has been publicly released for the investigation about the company’s financial meltdown. An employee is connected to all the employees she emailed. The second is more horizontal in nature, with no work hierarchies. We took users from different email newsgroups and connected them if they sent a message to the same thread. It’s the nerdy version of commenting on the same status update on Facebook. Differently from most communication network papers, we didn’t stop there. Every edge still carries some temporal information, namely the moment in which the email was sent. Above you have an extract of the network for a particular subject, where we have the email timestamp next to each edge.
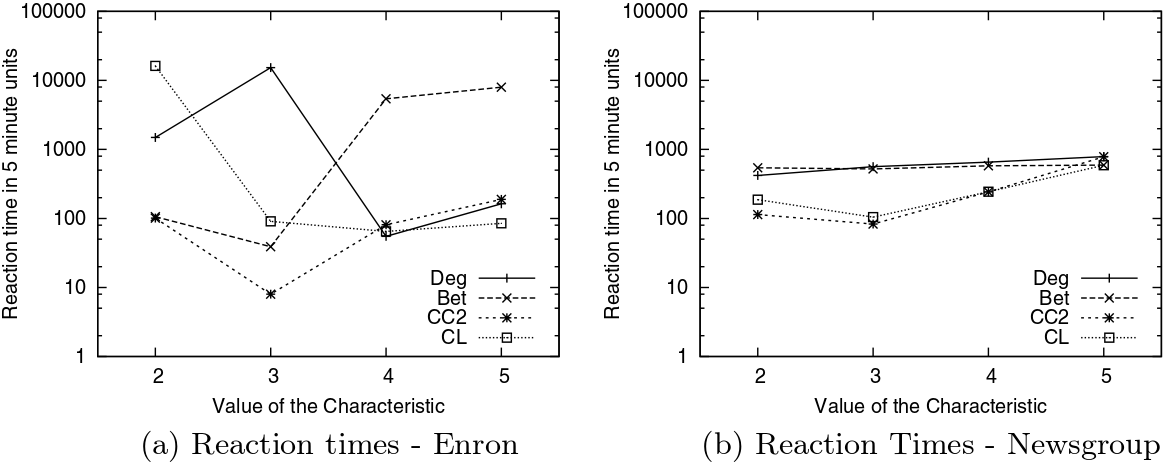
Here’s where the magic happens. With some data mining wizardry, we are able to tell the characteristic reaction times of different nodes in the network. We can divide these nodes in classes: high degree nodes, nodes inside a smaller community where everybody replies to everybody else and, yes, nodes with high betweenness centrality, our train station hubs. For every measure (characteristic), nodes are divided in five classes. Let’s consider betweenness. Class 1 contains all nodes which have betweenness 0, i.e. those through which no shortest path passes. From class 2 to 5 we have nodes of increasing betweenness. So, nodes in class 3 have a medium-low betweenness centrality and nodes in class 5 are the most central nodes in the network. At this point, we can plot the average reaction times for nodes belonging to different classes in the two networks. (Click on the plots to enlarge them)
The first thing that jumps to the eye is that Enron’s communications (on the left) are much more dependent on the node’s characteristics (whether the characteristic is degree or betweenness it doesn’t seem to matter) than Newsgroup’s ones, given the higher spread. But the interesting bit, at least for me, comes when you only look at betweenness centrality – the dashed line with crosses. Nodes with low (class 2) and medium-low (class 3) betweenness centrality have low reaction times, while more central nodes have significantly higher reaction times. Note that the classes have the same number of nodes in them, so we are not looking at statistical aberrations*. This does not happen in Newsgroups, due to the different nature of the communication in there: corporate in Enron versus topic-driven in Newsgroup.
The result carries some counter intuitive implications. In a corporate communication network the shortest path is not the fastest. In other words, don’t let your train pass through the central hub for a shortcut, ’cause it’s going to stay there for a long long time. It looks like people’s brains are less elastic than our train stations. You can’t add more platforms and personnel to make more things passing through them: if your communication network has large hubs, they are going to work slower. Surprisingly, this does not hold for the degree (solid line): it doesn’t seem to matter with how many people you interact, only that you are the person through which many shortest paths pass.
I can see myself trying to bring this line of research back from the dead. This premature paper needs quite some sanity checks (understatement alert), but it can go a long way. It can be part of the manual on how to build an efficient communication culture in your organization. Don’t overload people. Don’t create over-important nodes in the network, because you can’t allow all your communications to pass through them. Do keep in mind that your team is not a clockwork, it’s a brain-work. And brains don’t work like clocks.
* That’s also the reason to ditch class 1: it contains outliers and it is not comparable in size to the other classes.