Who will Cluster the Cluster Makers?
If you follow this blog, you know that I periodically talk about community discovery. The problem seems so deceptively simple: finding groups of nodes densely connected in a network. If it is so simple, why have I been talking about it since 2012? The reason is that it isn’t so simple, and people have tried to organize the literature explaining how the thousands of different algorithms work, how they perform, what definition of “community” they use. After all that work, I’m still left with one question. Which two algorithms return the same gosh darned communities in a network? That’s what we’re going to discover today.
What I want to do is to take as many community discovery algorithms as I can, test them on a set of networks, and compare their results to estimate how similar they are. This gives me a similarity matrix of algorithms, which I can transform into a network by keeping only similarities that are statistically significant. Once I have the network, I can discovery groups of algorithms returning a coherent set of results, because they’re all significantly related to each other. How do I find these groups? Well, by ehm…. er… performing… community… discovery? on the… network of… community discovery… algorithms… This is exactly the outline of my paper Discovering Communities of Community Discovery, which I presented at ASONAM last month.
“As many community discovery algorithms as I can” turned out to be 73, all implemented in different languages, taking input in different ways, and providing different output formats. I ran them on more than 1,500 networks (real world ones from ICON and synthetic benchmarks). It was a… difficult month for me. I compared their partitions by estimating their mutual information: given that I know the results of algorithm A, how much can I infer about the results of algorithm B? For each network where two algorithms result in a lot of mutual information, I increase their similarity count by one. Once I have all similarity counts, I can extract the backbone of this matrix, controlling for the fact that some algorithms tend to be more peculiar than others, while others tend to be more mainstream.
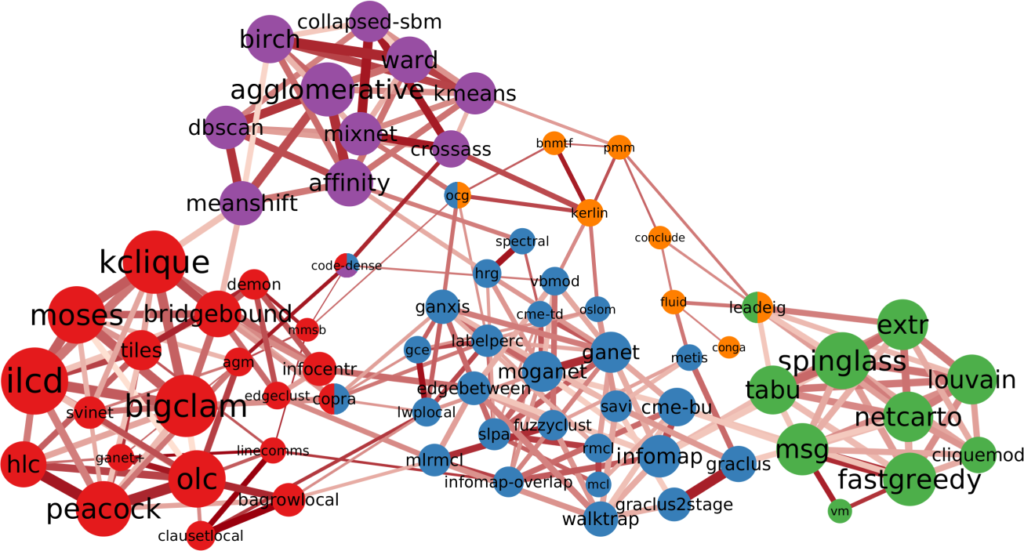
And this is the result (click to enlarge):
I love this network, because it has well defined groups and they all make sense. There’s the group of modularity maximization algorithms (in green), there’s the ones based on percolation / random walks (in blue), and the ones using neighbor similarity (in purple) as the guiding principle.
Then there’s a lump of algorithms that allow communities to share nodes (in red). The only thing these algorithms have in common is that they allow communities to share nodes, which is not a good enough common characteristics. The ways they find communities are as diverse as the ones you find in the rest of the network. But that’s the beauty of my approach: I can select a subset of nodes — say all overlapping community discovery algorithms — and re-apply the test of statistical significance with a more stringent threshold. This allows me to zoom in and see if there are meaningful structures inside the community. Lo and behold:
Here you can see meaningful groups of overlapping algorithms. There’s the ones achieving overlap by clustering edges instead of nodes (in blue), and the ones applying the percolation / random walk strategy (in green), but allowing for node sharing.
Why is this work significant? First, because it proves that there really are different — and valid — definitions of what communities are in complex networks. If there weren’t, this network would be more homogeneous, without distinct groups.
Second, as I mentioned, some of the networks I tested the algorithms on are standard benchmarks: LFR networks. These benchmarks grow a network with a planted community structure: the real latent structure the algorithm is supposed to find. Yet, this “ground truth” is well embedded in one of the clusters: the percolation/random walk community (in blue). LFR benchmarks follow that specific definition and not others. If you are developing a new community discovery algorithm which has a different community definition, you should not use the LFR benchmark to test it. Moreover, if you are developing a percolation/random walk algorithm and you’re correctly testing it on an LFR benchmark, you cannot test it against algorithms that are not part of the blue community. Otherwise the test would be unfair, because those algorithms are looking for something else: of course they’ll perform poorly on LFR benchmarks!
You can get the full list of algorithms that I tested, with proper references, from the official page of the project. From there, you can also download the network and use it for your purposes. This is necessarily an eternal work in progress: there are more than 73 community discovery algorithms out there. But I am but a man[citation needed] and I cannot spend my entire time scouting for implementations on the web. I got to put bread (or, preferably, pasta) on the table as well. Thus, if you think I really should have included your algorithm in this structure, you can mail me and send me a working implementation of it, and I’ll gladly run it on my benchmarks.
What’s next? I’d be delighted to inaugurate the field of meta-research. So join me, as I develop new projects such as:
- Predicting links of link predictors: which link prediction algorithms will become more similar in the future?
- Spreading epidemics of epidemic spreading: which researchers will cave in to peer pressure and publish a paper studying the diffusion of some phenomenon?
- Modeling the growth of growth models: how has the Barabasi and Albert model evolved over time? Which features were added? What about Watts & Strogatz’s model?
(In case you were wondering, I’m joking. In network science, sometimes that might be hard to tell.)
(Or am I?)
(It’s settled: the best among these papers will receive the hereby instituted Escher prize, awarded by Douglas Hofstadter himself)