Michele Coscia

Today I want to talk about jobs. Or, better, about finding a job. Sooner or later, this is a task that many people will have to perform and it is not usually a very enjoyable one. Writing a CV is mostly painful. You have to list all your skills, all the knowledge you have, what you have done in the past, the tasks you can perform. Everything to maximize your value to the eyes of the examiner, who is judge, jury and executioner of your working fate. But, after all, you can’t complain. You know the rules of the game. It is only fair, because the recruiter wants to see the best possible CV and the best possible CV is the one that includes the most relevant information: you have to stuff the maximum amount of skills in your body to maximize your value and it is the most valuable person the one who is going to be picked. Right?

Wrong. There’s one critical flaw to that reasoning, and that is time. Time is limited. You can’t spend too much time in stuffing knowledge into you, because there is too much knowledge out there and if you try to internalize everything you don’t have time to produce anything. This is not just my opinion. It is one of the cornerstones of widely accepted and useful theories, for example the division of labour. This is linked to the concept of “social knowledge“. Social knowledge is the collection of what people in society know. While personal knowledge is bounded by time, social knowledge is not, because many different brains work on it at the same time, making it grow beyond what any individual can grasp.

If you want to have 100 people to make cars, you don’t teach each one of them to make a car from scratch and then you watch them making 100 cars at the same time. Each guy will assemble one part. And he’ll be awesome at that particular part. This applies not only to manufacturing. How many times in your working life you found yourself struck with a problem, not exactly in your knowledge domain, and you solved it by simply asking someone about it? In my case, many. Think about how many times you Google something. That’s accessing the social knowledge of humanity. That is one of the reasons why, for example, the social return of education exceeds the private return.

The way you access social knowledge also changes the usefulness of it. It is better if a friend takes time to explain things to you than if you have to read an answer in Quora, that is also related only to some extent to your specific problem. Because tacit knowledge needs a broker to make it explicit and understandable. So it is better to have knowledgeable friends in many fields, or: your social network matters for your qualifications, because it’s the principal medium you use to get explicit knowledge from the tacit social knowledge.

So it seems like we are onto an interesting problem. On one hand, I hope to have convinced you that social knowledge is an important component of someone’s value; on the other hand that creates more questions than answers. How do we evaluate a person for a job? How do we measure the social knowledge she has access to? Well, if you know me you know what’s going to happen. A network algorithm, of course! Precisely, an algorithm with a flavor of Philip K. Dick in its name: UBIK, or “U know Because I Know”. This algorithm has been created and developed with the help of Giulio Rossetti, Diego Pennacchioli and Damiano Ceccarelli and has resulted in a paper published in the ASONAM 2013 conference that will take place later this month. Also, the code of UBIK is available for use.

Here’s how UBIK works. First, you have to start by collecting information about the social connections of people. It’s even better if you can find multiple types of connections from multiple sources, because the channel through which knowledge passes influences the quality of that knowledge. Second, for each person you have to collect their CV. Personal knowledge is still important. Once you have these pieces of information, UBIK can unweave its magic.

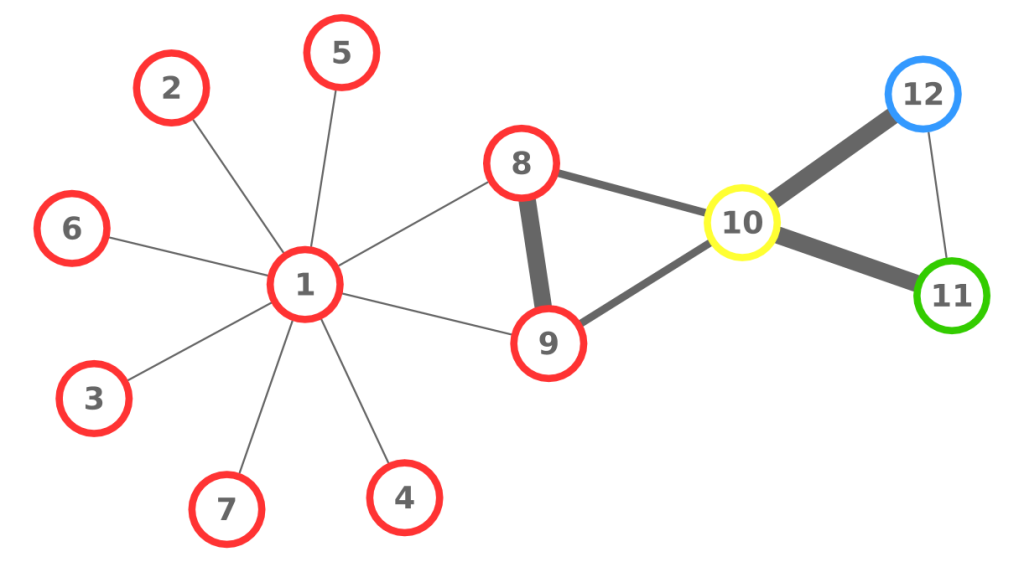
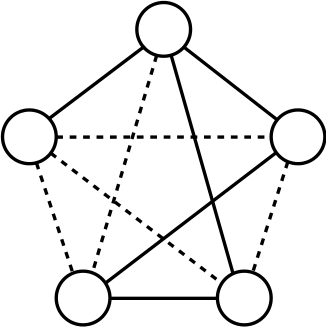
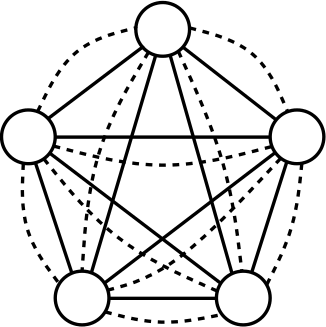
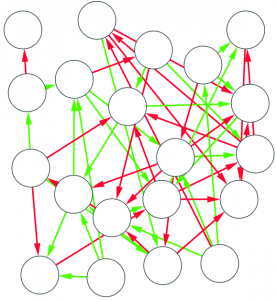
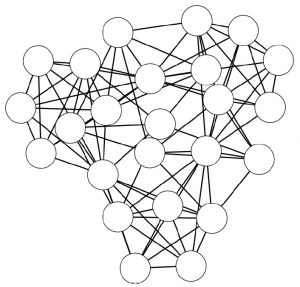
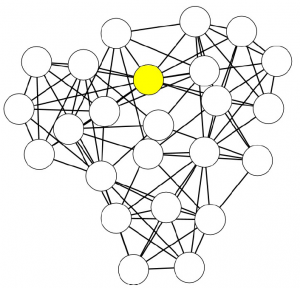
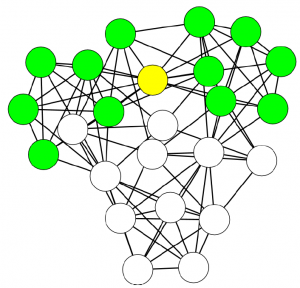
Let’s look at a simple example. The above picture can be considered a network of people: each node is a person, each person is connected to the people she knows, her color represents the skill in which she is specialized, and the width of the link is the strength of the connection (important: UBIK works with qualities of links, not strengths, but for the sake of simplicity in this example we use the latter). The consequence of our theory is that the skills of each person are transferred through the links of the network. Also, a direct connection is stronger than a connection through another node. For example, node 8 passes her skills more efficiently to 1 than node 10 does.

So, at the first iteration, UBIK passes the skills of each node to its neighbors. Node 1 gets a lot of red skill, node 10 gets all kinds of skills. It is a percolation process. At each iteration, UBIK keeps passing the entire set of updated skills, with an increasing penalty due to the social distance. I won’t bother you with the equations. Just know that, at some point, the penalty is so high that the algorithm stops.  The skill transfer happens proportionally to the strength of the links connecting the nodes. As a result, node 10 is super valuable, because she has access to the knowledge about all skills in the network, while for example node 1 will be a uber-specialist of the red skill. By just looking at their CV, it would be impossible to extract this information.

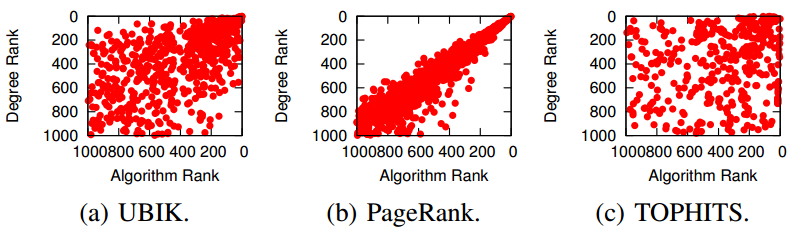
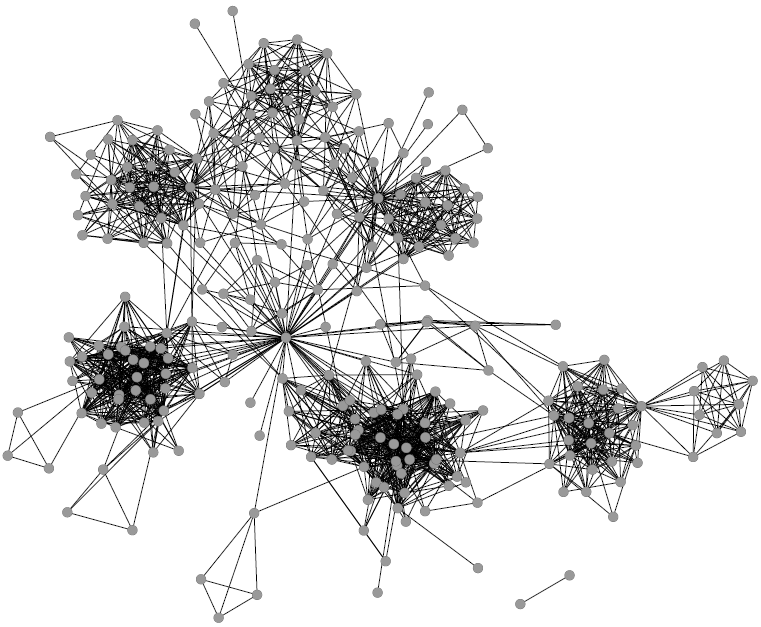
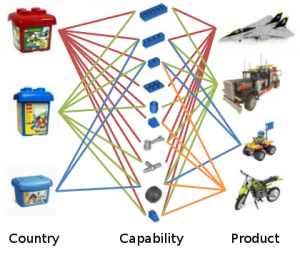
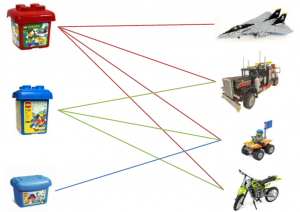
Some of you familiar with network analysis may have some bells ringing in their heads. “This is node ranking!” Well, yes. “So just use PageRank!” “Or HITS!” “Why do we need UBIK?” Well, for a number of reasons. First, UBIK handles multiple link types and multiple skills at the same time: (variants of) PageRank and HITS can do one or the other, but not so many can do it simultaneously yielding effective results. Second, PageRank and HITS have flaws. PageRank correlates with degree (the number of connections of a node) and centrality measures: see the above picture where we confront the rankings of the algorithms with the degree rank. HITS has similar flaws related to the nodes’ tendency of cluster in communities.

Moreover, when we applied the algorithms to network of researchers, UBIK was most likely to rank them in the same way as measures independent from networks such as the H-Index. This shows that UBIK may be more useful than other network ranking techniques when these independent evaluation criteria are not available. The beauty of UBIK consists in multiple rankings. Below I report some rankings of researchers in Computer Science. Each number is the rank that UBIK gave to the researcher in a particular conference. Each conference is a different ranking that UBIK is able to distinguish. We are able to spot the specialists of many computer science conferences, highlighting their prominence in one community and low ranking in others. Also, we report the rankings in these conferences for the most prominent general authors, showing that they rank on average well in many different venues, but they are not really specialists.

And that’s why you should give UBIK a chance.

Continue Reading

As I mentioned a couple of months ago, during the first week of June the NetSci conference took place. NetSci is the main venue that brings together all researchers interested and involved in network science. It has always been a gigantic opportunity to put you in contact with the big shots in network analysis and an excellent playground for very interesting discussions. This year was no different.

Of course, for me the most important part of it was the very first day, when the satellite on multiple networks (organized by myself together with Matteo Magnani, Dino Pedreschi, Luca Rossi, Guido Caldarelli and Przemyslaw Kazienko) happened. As I wrote more than once in the past, multiple networks are networks in which the nodes may be connected with different kinds of interactions (friendship, collaboration, and so on).

It was an extremely interesting event; a first step to bring together many researchers working on the topic of multiple networks, most of whom hadn’t spoken to each other up until then. And when I say it was a smooth and successful operation, you don’t have to take my word for it. We have proof of a room full of brilliant minds taking up all the available spots… and beyond:

The talks were very impressive:

• We learnt how to measure eigenvector centrality on multiple networks (and you can too);
• We learnt how to extend basic measures from regular complex networks to multiple networks (and you can too);
• We learnt how to mine network with heterogeneous information on nodes and edges (and you can too);
• We learnt how to detect communities on multiple networks (and you can too);
• We learnt how to infer the latent structure of inter-related networks (and you can too);
• We learnt how a random walker behaves on dynamic networks (and you can too);
• We learnt about the structure and dynamics of multiple networks (and you can too);
• And we learnt how the properties of multiple networks arise when adding one network at a time (and you can too).

But NetSci, of course, was much more than just this satellite. Another event you absolutely didn’t want to miss there was the Arts, Humanities and Complex Networks Symposium, organized by Max Schich and Isabel Meirelles.

They are both great guys, with a gigantic knowledge about art and design. For example, they picked up a great reference for the logo of their symposium, namely one of the most known infographics made about visual arts, by Alfred Barr:

And besides the usual great lineup of talks (from the Wikidata project to a very cool movie ranking multiple network algorithm) you can learn surprising stuff about basically everything. My favorite: the observation of one of the speakers about the above visualization itself. Apparently, he was the first to realize that there is a bull up there (hint: Cubism lays in between the bull’s horns). As Max then puts it:

Then… the rest of the conference. It is impossible to even give a close idea of the overload of ideas and flashes of genius that populated the venue for those three days. I’ll work around the problem and cheat by giving you a laundry list of (a very tight subset of) the things that most impressed me during the conference:

• The excellent invited talk by Shlomo Havlin about interdependent networks (networks which depend on each other to function, much like a computer network controlling the electric grid). This interests me because he claims that interdependent networks are a more general case of multiple networks (although I personally have an inkling that perhaps they can be reduced to the same model);
• The usual spectacular presentation style of my friend Cesàr Hidalgo, who this time talked about a complex system showing a nested structure: namely, the cultural exports of different countries;
• A really great contributed talk by Esteban Moro, which in my opinion could have been a keynote speech as well. Dr. Moro highlighted how people have a trade-off between social capacity (how many relationships we can keep alive) and social activity (how many new people we can meet). As a consequence, different social strategies arise;
• A brilliant mathematical formulation of a network problem by Jure Leskovec, that, in my opinion, could be the final word about the problem itself. And it resembles the formal mathematical formulation of the same algorithmic idea behind my DEMON;
• And the hilarious ignite talks, 5 minutes and 20 slides for each speaker. There was no possibility of interacting, with the presentation automatically jumping to the next slide every 15 seconds. Next year I definitely want to try to do one too.

And, of course, many other things. But you get the idea: blog posts about it are boring, you really have to experience it yourself.

Continue Reading

This month, I am interrupting the sequence of posts discussing my papers for a shameless self-promotion – after all, this entire website is shameless self-promotion, so I don’t see a problem in what I’m doing. Some months ago, I discussed my work on multidimensional networks, networks that include different kinds of relations at the same time. The whole point of the post was that these are different animals than traditional complex networks, and thus they require new tools and a new mindset.

So I asked myself: “What is the best way to create this new sensibility in the network community?”. I also asked a bunch of other great people, in no particular order: Matteo Magnani, Luca Rossi, Dino Pedreschi, Guido Caldarelli and Przemyslaw Kazienko. The result was the topic of today’s post: a symposium in the 2013 edition of the NetSci conference!

NetSci is a great venue for network people. From their website:

“The conference focuses on interdisciplinary research on networks from various disciplines such as economy, biology, medicine, or sociology, and aims to bring new network analytic methods from physics, computer science, math, or statistics to the attention of a large and diverse audience.”

This year, NetSci will take place in Copenhagen and you should check out a number of reasons for attending. One of those reasons is our symposium, called “Multiple Network Modeling, Analysis and Mining“. You can check important information about attending the symposium in the official event webpage: http://multiplenetworks.netsci2013.net/. Here are the three main highlights:

• It is an excellent occasion to learn more about multidimensional networks, a model that can help understand the complex interplay between the different relationships we establish every day (friendship, collaboration, club membership, …), better than everything else has been done before;
• We still have to finalize our speaker list, but it will be of very high quality and will include Jiawei Han, Lei Tang, Renaud Lambiotte and others;
• Symposium attendance is free! And there will be free food! Woo-hoo! Just sign up in the official Google Doc.

Don’t take my word on the first point and check out the publications we refer to in our webpage. Here, following the above mentioned shameless self-promotion, I’ll list the papers on the subject written by yours truly:

• Berlingerio, M., Coscia, M., Giannotti, F., Monreale, A. and Pedreschi, D., Multidimensional networks: foundations of structural analysis. In World Wide Web Journal, 2012.
• Berlingerio, M., Coscia, M., Giannotti, F., Monreale, A. and Pedreschi, D., The Pursuit of Hubbiness: analysis of hubs in large multidimensional networks. In Journal of Computational Science, 2011.
• Berlingerio, M., Coscia, M., Giannotti, F., Monreale, A. and Pedreschi, D., Foundations of Multidimensional Network Analysis. In ASONAM, 2011.
• Berlingerio, M., Coscia, M., Giannotti, F., Finding and Characterizing Communities in Multidimensional Networks. In ASONAM, 2011.

If you find all of this interesting, I definitely hope to see you in Copenhagen this June!

Continue Reading

I decided to give to this blog post an obscure title because today I want to talk about something that in complex network analysis goes under many names, so I did not want to favor any of them. What I am talking about are networks with multiple types of relations in them, the main subject of my PhD Thesis and of a recent article that I published in the World Wide Web Journal. These structures are putting more complexity on top of complex networks, therefore they are complex network squared: hence the fancy blog title.

These networks are referred to in the literature with the following terms:

• Multidimensional (the term that I use in my thesis);
• Multirelational;
• Layered;
• Interdependent;
• Multisliced;
• Multilevel;

and so on and so forth. All these terms refer to the same theoretical object, that is also implemented in many ways. I’ll mention some of them just to sound like the guardian of an obscure cult: labeled multigraphs, hypergraphs, mesostructures and coupling edges.

Despite the confusion that I tried to create with the first paragraphs, the general idea of this line of research is brutally simple: in our everyday life we are not part of only one network. It may look like we are, but when we start thinking harder about our relationships, we realize that we know the people we know for different reasons. This idea is the one behind the fact that every person can belong to different “communities” at the same time, which I already discussed in these pages. But it is deeper than that. It does not only require the more sophisticated, but still traditional, community discovery algorithm that I described in that blog post. It requires a whole new model and mindset.

Before multidimensional networks (forgive me if for clarity I’ll use my term for these structures) the classical complex network analyst would just assume that a single relation represents a particular phenomenon and nothing else can be said about it. Allow me to recycle this picture about my Facebook friends:

Intuitively this looks nice, as we can find communities and central nodes. But is this picture really telling us everything about my Facebook friends? What about a higher order of aggregation among them? What about not only their friendship links but also their common interests? The multidimensional network analyst throws a bunch of new connections on top of it and she tells you: “There’s something more”. In this case:

A visualization that is not nearly as elegant as the previous one, I give you that, but nevertheless it is useful to understand a higher level aggregation of my Facebook friends. On top of the connections between friends, we added edges connecting people if they are part of the same group or if they like the same stuff on Facebook. The two gigantic hairballs are composed by people who are in the same location: there is the cluster of people living in Italy, the one of people living in the US, and connections between them from people travelling between the two countries. So, we saw that adding different types of relations uncovers structural properties that none of the relations by itself would reveal.

I’ll give you another example of a cool real world effect of multidimensional networks. This is not from a work of mine, but it is from the Nature paper “Catastrophic cascade of failures in interdependent networks” by  Sergey V. Buldyrev, Roni Parshani, Gerald Paul, H. Eugene Stanley and Shlomo Havlin. Suppose you have a power grid: what happens if one plant is subject to a failure? The classical complex network analyst tells you that we could not care less: the power grid is a scale free network, in which the majority of plants are only connected to a couple other plants. So, a random failure of one plant does not affect the rest of the network too much, unless we are extremely unlucky and we lose a power hub (but that’s really rare, and the classical network guy is an incurable optimist).

A multidimensional network scientist, instead, is way more careful. Why? Because he knows that the power grid network is not independent from everything else, but it is plugged into another network. For example, in a computer network that regulates its functioning. When a power plant goes down, a set of computers cannot work anymore. And what happen to the plants that are connected to those computers? They fail too, triggering another computer failure and God helps us all. It is theoretically proven that two different scale free relations, dependent on each other, are much much much more fragile than a single scale free network. This actually happened in Italy (where else?) and the following is a depiction from Buldyrev et al’s paper:

In the first Italy we see one plant going down (in red on the map) taking with it the computers it supplies with energy (in the flying network). This triggers a couple more failures in the second picture that eventually, in the third picture, completely destroy the power supply chain of southern Italy.

So far I gave you the idea that multidimensional networks are not exactly the same animal as classical complex networks. To give you a taste of how to prove this, I’ll spare you the super complicated equations of interdependent network percolation present in the Nature paper. I’ll instead provide another example from community discovery. As I said in my previous post, community discovery is loosely defined as the problem of grouping nodes in a network that are “densely connected”. Naturally, when we deal with multidimensional networks, the “densely connected” has to be changed into “multidimensionally densely connected”. Why is this challenging? Here I’ll give you an intuition and I promise that in the future I’ll come back with more details. For now, it is sufficient to use two pictures. Here’s the first:

Here we assume that we have two different dimensions and they are represented with solid or dashed edges. Is this set of nodes multidimensionally dense? Of course: everybody is connected with everybody and all dimensions of the network are equally represented. Now consider another situation:

Is this set of nodes multidimensionally dense? Of course: everybody is connected with everybody and all dimensions of the network are equally represented. But the two examples are very different. That’s funny: we just discovered that, in multidimensional networks, density is an ambiguous concept.

And, as conclusion, I’ll add some multidimensional flavor to another classical network problem: link prediction. Link prediction aims at predicting your next Facebook friend. The above mentioned multidimensional network scientist steps in and says: “But why only your next Facebook friend? Why not your next virtual acquaintance tout-court?”. He means that all your social media connections and their different types play a role in determining when and where you’ll connect with somebody. This is exactly what multidimensional link prediction is, and how to do this is a complex problem that currently remains unsolved. But the multidimensional network guy loves complex problems as much as he loves complex words.

Continue Reading

As reported in different parts of this website, the group I am currently working in is called “Center for International Development”. The mission of this group, in the words of its head Ricardo Hausmann, is quite trivial and unambitious: to eradicate poverty from the world. Knowing how to do it is far from easy and there are different schools of thought about it. The one that Hausmann chose starts with understanding how production and economic growth work, i.e. why some industries are successful in a country and not in another.

To address this question, Hausmann (together with César A. Hidalgo, Bailey Klinger and Albert-Laslo Barabasi) developed the Product Space. The original idea has been published in this paper in 2007, far before I joined the group, but my (overestimated) expertise was heavily exploited to generate its current implementation (the Atlas of Economic Complexity, a book freely available in electronic format). For this reason I feel no shame in writing a post about it in this blog (and to share the Product Space itself in my Dataset page).

The fundamental assumption of the Product Space is the following: countries are able to have a comparative advantage in exporting a given product because they have the capabilities to export it. In abstract, it means: “I do this, because I can“. Quite reasonable. In pictures, with the awesome “A capability is a piece of LEGO” metaphor created by Hidalgo:

From this assumption, it follows that if a country can export two different products, it is because it has the capabilities to export both. Also this step is quite easy. The conclusion is immediate: a country’s development success is lead by its capabilities. The more capabilities the country has (meaning that its LEGO box is big and it contains a lot of pieces), the more capabilities it will be able to acquire, the faster it will grow.

There is a small problem with this conclusion: we can’t observe the capabilities. Of course, if we could then they would be blatantly obvious, so every country could employ its growth strategy based on them. (There is actually another problem: capabilities are tacit knowledge, as Nonaka and Takeuchi would say, so you really can’t teach them, but we will come to this problem later)

What we can observe is simply which countries export what:

But remember: if two products are exported by the same country, then there may be common capabilities needed for their productions; while if two countries export the same products, then they share at least part of the same capabilities. In mathematical terms, it means that the observed country export picture is actually the multiplication of the two halves of the second picture of the post, or:

This is nice because it means that we can collapse the country-product relationships into product-product relationships and then mapping which product is related to which other product, because it requires the same capabilities. The advice for countries is then: if you are exporting product x, then you are likely to have most of the capabilities to export all the products that are connected to x. And this is how the Product Space was born, a single picture expressing all these relationships:

(click on the picture for a higher resolution, or just browse the Atlas website, that is also dynamic).

In the picture the nodes are colored according to the community they belong to (for more information about communities, see a previous post). The communities make sense because they group products that intuitively require the same extended set of capabilities: in cyan we have the electronic products, light blue is machinery, green is garments and so on and so forth.

Is the structure of the Product Space telling us something reliable? Yes, countries are way more likely to start export products that are close, in the Product Space, to the products they already export. Also, it is important to know where the export products of a country are in the Product Space. The more present a country is in the denser cores of the Product Space, the more complex it is said to be. This measure of complexity is a better predictor of GDP growth than classical measures used in political economy like average years of schooling.

Is the structure of the Product Space telling us something interesting? Hell yeah, although it’s not nice to hear. The Product Space has communities, so if you export a product belonging to a community then you have a lot of options to expand inside the community. However, many products are outside the communities, and they are very weakly connected with the rest, often through long chains. The meaning? If you are only exporting those products, you are doomed to not grow, because there is no way that you’ll suddenly start exporting products of a community from nothing (because this would require tacit knowledge that you cannot learn and is not close to what you know). And guess what products the poorest countries are currently exporting.

To conclude, a couple of pictures to provide one proof of the reasoning above. In 1970, Peru had more average years of schooling, more land and twice the GDP per capita of South Korea. Traditional political economy would say that Peru was strong and there was no way that South Korea could catch up. Where South Korea is today is evident. What was the difference between the two countries in terms of Product Space?

(again, click for higher resolution. The black square border indicates which products the country is exporting). There is not a lot of difference in quantities (and this explains why South Korea was poorer). However, South Korea had those two or three products in a very valuable position, while Peru had only products in the branches: a long way to the core. In 2003, this was the result:

Peru is still mainly on the edges, South Korea occupies the center. And that’s all.

Continue Reading

Imagine being subscribed to a service where you can read other users’ opinions about what interests you. Imagine that, for your convenience, the system allows you to tag other users as “reliable” or “unreliable”, such that the system will not bother you by signaling new opinions from users that you regard as unreliable, while highlighting the reliable ones. Imagine noticing a series of opinions, by a user you haven’t classified yet, regarding stuff you really care about. Imagine also being extremely lazy and unwilling to make up your own mind if her opinions are really worth your time or not. How is it possible to classify the user as reliable or unreliable for you without reading?

What I just described in the previous paragraph is a problem affecting only very lazy people. Computer Science is the science developed for lazy people, so you can bet that this problem definition has been tackled extensively. In fact, it has been. This problem is known as “Edge Sign Classification”, the art of classifying positive/negative relations in social media.

Computer Science is not only a science for lazy people, is also a science carried out by lazy people. For this reason, the edge sign classification problem has been mainly tackled by borrowing the social balance theory for complex networks, an approach that here I’m criticizing (while providing an alternative, I’m not a monster!). Let’s dive for a second into social balance theory, with the warning that we will stay on the surface without oxygen tanks, to get to the minimum depth that is sufficient for our purposes.

Formally, social balance theory states that in social environments there exist structures that are balanced and structures that are unbalanced. The former should be over-expressed (i.e. we are more likely to find them) while the latter should be rarer than expected. If these sentences are unclear to you, allow me to reformulate them using ancient popular wisdom. Social balance theory states mainly two sentences: “The friend of my friend is usually my friend too” and “The enemy of my enemy is usually my friend”, so social relations following these rules are more common than ones that do not follow them.

Let’s make two visual examples among the many possible. These structures in a social network are balanced:

(on the left we have the “friend of my friend” situation, while on the right we have the “enemy of my enemy” rule). On the other hand, these structures are unbalanced:

(the latter on the right is actually a bit more complicated situation, but our dive in social balance is coming to an abrupt end, therefore we have no space to deal with it).

These structures are indeed found, as expected, to be over- or under-expressed in real world social networks (see the work of Szell et al). So the state of the art of link sign classification simply takes an edge, it controls for all the triangles surrounding it and returns the expected edge (here’s the paper – to be honest there are other papers with different proposed techniques, but this one is the most successful).

Now, the critique. This approach in my opinion has two major flaws. First, it is too deterministic. By applying social balance theory we are implying that all social networks obey to the very same mechanics even if they appear in different contexts. My intuition is that this assumption is rather limiting and untrue. Second, it limits itself to simple structures, i.e. triads of three nodes and edges. It does so because triangles are easy to understand for humans, because they are described by the very intuitive sentences presented before. But a computer does not need this oversimplification: a computer is there to do the work we find too tedious to do (remember the introduction: computer scientists are lazy animals).

In the last months, I worked on this problem with a very smart undergraduate student for his master thesis (this is the resulting paper, published this year at SocialCom). Our idea was (1) to use graph mining techniques to count not only triangles but any kind of structures in signed complex networks. Then, (2) we generated graph association rules using the frequencies of the structures extracted and (3) we used the rules with highest confidence and support to classify the edge sign. Allow me to decode in human terms what I just described technically.

1) Graph mining algorithms are algorithms that, given a set of small graphs, count in how many of the graphs a particular substructure is present. The first problem is that these algorithms are not really well defined if we have a single graph for which we want to count how many times the structure is present*. Unfortunately, what we have is indeed not a collection of small graphs, but a single large graph, like this:

So, the first step is to split this structure in many small graphs. Our idea was to extract the ego network for each node in the network, i.e. the collection of all the neighbors of this node, and the edges among them. The logical explanation is that we count how many users “see” the given structure around them in the network:

(these are only 4 ego networks out of a total of 20 from the above example).

2) Now we can count how many times, for example, a triangle with three green edges is “seen” by the nodes of the network. Now we need to construct the “graph association rule”. Suppose that we “see” the following graph 20 times:

and the following graph, which is the same graph but with one additional negative edge, 16 times:

In this case we can create a rule stating: whenever we see the former graph, then we know with 80% confidence (16 / 20 = 0.8) that this graph is actually part of the latter one. The former graph is called premise and the latter is the consequence. We create rules in such a way that the consequence is an expansion of just one edge of the premise.

3) Whenever we want to know if we can trust the new guy (i.e. we have a mysterious edge without the sign), we can check around what premises match.  The consequences of these premises give us a hunch at the sign of our mysterious edge and the consequence with highest confidence is the one we will use to guess the sign.

In the paper you can find the details of the performance of this approach. Long story short: we are not always better than the approach based on social balance theory (the “triangle theory”, as you will remember). We are better in general, but worse when there are already a lot of friends with an expressed opinion about the new guy**. However, this is something that I give away very happily, as usually they don’t know, because social networks are sparse and there is a high chance that the new person does not share any friends with you. So, here’s the catch. If you want to answer the initial question the first thing you have to do is to calculate how many friends of yours have an opinion. If few do (and that happens most of the time) you use our method, otherwise you just rely on them and you trust the social balance theory.

With our approach we overcome the problems of determinism and oversimplification I stated before, as we generate different sets of rules for different networks and we can generate rules with an arbitrary number of nodes. Well, we could, as for now this is only a proof of principle. We are working very hard to provide some usable code, so you can test yourself the long blabbering present in this post.

* Note for experts in graph mining: I know that there are algorithms defined on the single-graph setting, but I am explicitly choosing an alternative, more intuitive way.

** Another boring formal explanation. The results are provided in function of a measure called “embeddedness” of an edge (E(u,v) for the edge connecting nodes u and v). E(u,v) is a measure returning the number of common neighbors of the two nodes connected by the mysterious edge. For all the edges with minimum embeddedness larger than zero (E(u,v) > 0, i.e. all the edges in the network) we outperform the social balance, with accuracy close to 90%. However, for larger minimum embeddedness (like E(u,v) > 25), social balance wins. This happens because there is a lot of information around the edge. It is important to note that the number of edges with E(u,v) > 25 is usually way lower than half of the network (from 4% to 25%).

Continue Reading

When thinking about our social life, we instinctively recall the reason why we know the people we know. There is my sister, there’s the friend with whom I shared all my experiences – from stealing snacks at the primary school to the bachelor thesis we wrote together – and finally there’s that obscure guy who I don’t really know but he added me on Facebook and I don’t want to reduce my friend counter. A long time ago a very nice app called Nexus allowed Facebook users to visualize this concept. Nexus then died, it was replaced by Social Graph, which died too. Now you can use Touch Graph, but it is not nearly as good and, besides this, it’s a different story from the one I want to tell.

Nexus’ visualizations looked more or less like this:

The grey dots are my friends on Facebook and they are connected if they are friends on Facebook too. It’s clear that people you know for the same reason are densely connected to each other, because they are very likely to know each other too. The structure is pretty spectacular, I have to admit. It also seems to make a lot of sense and these different dense areas (“communities”) do not look too hard to be extracted automatically by an algorithm.

It’s on the shoulders of this gigantic positivist naïvety that countless authors decided to write such algorithm. Soon enough, a new branch of complex network analysis was born, called Community Discovery. The aim of  community discovery is to group nodes that are densely connected to each other. The groups are then called “communities” and nodes are said to be “members” of a community. Community discovery has a long, long history made by initial successes, coups de théâtre, drama and romance, but it is a complicated story and not in the scope of this post. Basically, many authors realized that they were dealing with a larger mess than previously thought. The main reason is that most, if not all, real world networks do not look like the above example. At. All. They look like this:

An ugly and meaningless hairball. Most people scratched their heads and decided to stick with their definition of community. This is the wrong way because it implies that we just give up in analyzing the second case and we consider the two examples as completely different phenomena. Guess what: they are not. The second network, too, is a sample of the Facebook friendship network and it contains the first. The sole difference between the two is the scale: the first only considers the immediate neighborhood of a node (me), the second just samples 15,000 users and the connections between them.

It’s on the basis of these considerations that I wrote a paper on community discovery, together with my co-authors at the KDDLab in Italy. We developed an algorithm that exploits the order at the local level around a node to find a sense of the connective mess at the global scale. It is called DEMON: Democratic Estimate of the Modular Organization of a Network.

The details of the implementation are included in the paper accepted at the SIGKDD 2012 conference on Data Mining. It was recently presented there by my co-author Giulio Rossetti who also happens to have written its implementation, freely available (and Open Source!). In this post, I’ll just give you a quick idea about how DEMON works.

Let’s consider a simple, messy, network:

It looks more like the messy hairball, doesn’t it? Let’s now select a node:

And then all the other nodes that are directly connected to it:

Now, let us ignore all the other nodes of the network, included the first selected. We just create a network only using the green nodes and the connections between them. What does this network look like? Like this:

Surprise! We’ve fallen back into the first, neatly divided, example. Now what we need to do is to just apply a very simple, old-school, community discovery algorithm to this sample and we have an idea about the communities surrounding the yellow node. We apply this operation to all the nodes of the network and then we merge together the communities that share an extensive portion of their members. I won’t bother you with the details and the proofs about how awesome this method is and how it outperforms the current state-of-the-art community discovery algorithms because everything is in the paper and I don’t like to brag (twice).

Continue Reading