Michele Coscia

The literature about community discovery, which deals with the problem of finding related groups of nodes in a network, is vast, interesting and full of potential practical applications. However, if I would have to give one critique of it, it would be about its self referential character. Most community discovery papers I read in computer science and physics journals are mainly about finding communities. Not much time is spent thinking about what to do with them, or what they mean. My first post in this blog was about a community discovery algorithm. Recently, an extended version of that paper has been accepted in a computer science journal. Since that first post, I (mainly) added some crucial modifications and features to the algorithm. I don’t want to talk about those here: they are boring. I also didn’t bring up this paper to boast about it. Okay, maybe a little. I did it because the paper touches upon the issue I am talking about here: it tries to do something with communities, it tries to explain something about them. Namely, it asks: why do communities overlap?

First of all: communities do overlap. When trying to detect them, many researchers realized that hard partitions, where each node can belong to one and only one community, are not always a good idea. Most of them found this a problem. Others were actually very happy: the problem gets harder! Nice! (Researchers are weird). Blinded by their enthusiasm, they started developing algorithms to deal with this overlap. Not many asked the question I am trying to answer here: why do communities overlap? As a result, some of these algorithms detect this overlap, but using approaches that do not really mean anything in real life, it’s just a mathematical trick. Others, instead, build the algorithm around a core hypothesis.

This hypothesis is nothing unheard of. Communities overlap because people have complex lives. Some of your college mates also attend your yoga class. And you know your significant other’s colleagues, which puts you in their community. All these communities have you as common member, and probably some more people too. The beauty of this is that it is not only intuitive: it works well in finding communities in real world social networks. So well that it is the assumption of my approach and of many others outstanding algorithms (this and this are the first two that pop into my mind, but there are probably many more). Another beautiful thing about it is that it is almost obvious, and so it is probably true. But here we hit a wall.

The fact that it is simple, reasonable and it works well in practice proves nothing about its property of being true. There are things that are not simple nor reasonable, but nevertheless true (hello quantum physics!). And there is practical knowledge that does not quite correspond to how things work (in my opinion, most computer science is a patch and nobody really knows why it works). Unless we test it, we cannot say that this nice practical principle actually corresponds to something happening in reality. So how do we go on and prove it? In the paper I proposed a first step.

This brings me back to another old love of mine. Multidimensional networks. They are networks in which we put multiple relations in a cage together in mating season and see what happens (research is fun). The idea behind the paper is that multidimensional networks give us the perfect tool to test the hypothesis. In monodimensional networks you have no clue why two people are connecting besides the obvious “they know each other”. In a multidimensional network, you know why they know each other, it’s information embedded in the type of the relation. So, the hypothesis is that different types of relations are the cause of the community overlap, and with multidimensional networks we can look at how communities distribute over relations. First, let us take a look at what two overlapping communities look like in a multidimensional network.

We collected a multidimensional social network putting together relationships between users in Facebook, Twitter and Foursquare. We then used DEMON to extract overlapping communities from each dimension. We then took two communities with extensive overlap in the Facebook dimension (picture below).

We then looked at the very same set of nodes, but now in the Foursquare network. In the picture below, we kept the edges, and the node positioning, of the Facebook network to make the comparison easier, but keep in mind that the edges in the Foursquare dimension are different, and they are the ones that decide to what community the nodes belong.

Very interesting. The communities look a lot alike, although the shared (and non shared) nodes are slightly different. Now node 7369 is shared (it wasn’t in Facebook) while node 8062 isn’t (whereas it was before). Let’s put another nail on the coffin and see the communities these nodes belong in Twitter (same disclaimer applies):

Surprise surprise, in Twitter there is actually only one community, which brings together the majority of the nodes of the two communities. So here’s where our overlap comes from: common affiliations in different dimensions! Now, I’m going to deal with that voice in your head that is screaming “Anecdotal! Anecdotal!”. (You don’t hear it? Did I already mention that researchers are weird? In any case “Anecdotal” refers to a type of evidence that bears no value in scientifically proving a point if not backed by more solid proofs). Put in a more general way: the more two communities overlap in some dimension, the more likely it is we can find a dimension in which these communities are actually a single community. This involves boring details you can find in the paper which ultimately generate this plot:

Does this plot prove our theory without leaving out any reasonable doubt? Maybe, or not really. There are still things to check. But science is made by tiny steps forward. And this is certainly one.

You know that I am a guy deeply involved in multiple networks, networks containing different types of relations. You probably also remember that last year I organized, with Matteo Magnani, Luca Rossi, Dino Pedreschi, Guido Caldarelli and Przemyslaw Kazienko, a symposium on such a fascinating mathematical model and its applications (my report on it). Well: it is going to happen again at the 2014 edition of NetSci.

Some things changed since last year. Let me start from the most important. This year we are open to contributed talks! Last year the speakers where invitation-only: we were just starting and we wanted to understand what kind of crowd we had. The response was positive for the event and negative for the poor guy (me) who had to find extra chairs to accommodate the larger-than-expected bunch of people who showed up. So, choose your best work on multiple (multiplex, multidimensional, multilayer, multirelational… whatever!) networks and send a 300-word abstract and a figure here: https://www.easychair.org/conferences/?conf=mnam2014. You have time until April 14th, and you will receive notification of acceptance in two weeks, April 28th.

We are still going to have exciting keynotes, of course. So far, the first confirmed speaker is Renaud Lambiotte. If you read this blog, chances are that you are already familiar with the outstanding work he is doing in network science.

The date of the event didn’t change, it is still the first week of June (UPDATE: the exact day the satellite will take place is June 2nd, for the entire day). The location, of course, did: it is going to happen in Berkeley California, at the Claremont Hotel and the Clark Kerr Campus of the University of California. We go where NetSci goes, and with a reason: NetSci is the premier venue if you are interested in network science. And we want to play with the coolest kids, don’t we?

Two other things did not change and are worth remembering. First, participation is free of charge. We are interested in your brains, not your wallets. (UPDATE: Apparently, even if you are just attending this satellite, NetSci’s organizers require you to register anyway. Rates and information are here. Early registration is April 4th. Here, we are still interested just in your brains, though 🙂 ). Second, we are still asking you to tell us if you are planning to come to the event. It is mostly a selfish maneuver: I want to limit my quests in finding extra chairs to the minimum. For this reason, we set up this handy and quick Google form for you.

So, don’t forget to send us an abstract. And see you in just a couple of months in Berkeley!

New year, old topic. I could make a lot of resolutions for this new year, but for sure to stop talking about community discovery is not among them. At least this time I tried to turn it up a notch in the epicness of the title. My aim is to give some substance to one of the many typical filler phrases in science writing. The culprit sentence in this case is “different application scenarios demand different approaches”. Bear with me for a metaphoric example.

When presenting a new toaster, it is difficult to prove that it toasts everything better under any point of view, under any circumstances. It usually does most toasts okay, and for one kind of toasts it really shines. Or its toasts really suck, but it can toast underwater. That’s fine. We are all grown up here, we don’t believe in the fairy tales of the silver bullets any more. At this point, our toaster salesman is forced to say it. “Different application scenarios demand different approaches”. In some cases this is a shameful fig leaf, but in many others it is simply true. Problem is: nobody really checks.

I decided to check. At least one of them. Teaming up with Diego Pennacchioli and Dino Pedreschi, I put the spotlight on one of the strongest dichotomies in community discovery.  As you may remember, community discovery algorithms can force every node to belong to just one community, or allow them to be in many of them. The former approach is called “graph partitioning”, whilst the latter aims to find an “overlapping coverage”. Are these two strategies yielding interesting, yet completely different, results? This question has been dissected in the paper: “Overlap Versus Partition: Marketing Classification and Customer Profiling in Complex Networks of Products“, that will be presented in one workshop of the 2014 edition of the International Conference of Data Engineering.  Let me refresh your mind about overlaps and partitions.

Above you have the nec plus ultra scenario for a partitioning algorithm. If a partitioning algorithm sees the graph on the left, it would just die of happiness. In the graph, in fact, it appears very clearly that each node belongs to a very specific community. And it can’t belong to any other. If we assume that our algorithm works on edge strength (e.g. the inverse of the edge betweenness), then what the algorithm really sees is the graph on the right. It then proceeds to group together the nodes for which the edge strength is maximal, et voilà.

Here we have an example that’s a bit more complex. The picture has too many overlapping parts, so let me describe the connection pattern. In the graph on the left there are several groups of 6 nodes, each node connected to all other members of the group. In practice, each diagonal is completely connected to the two neighbouring diagonals. Clearly, here there is no way we can put each node in a disjoint group. Why put together nodes 0,1,2 with 3,4,5 and not with 9,10,11? But at that point, why 9,10,11 should be in a community with them and not with 6,7,8? The correct approach is just to allow every completely connected group to be a community, thus letting nodes to be part of more than a community. Some overlapping algorithms see the graph as it has been depicted on the right, with an edge colour per densely connected group.

Time to test which one of these approaches is The Right One! For our data quest we focused on supermarket transactions. We created a network of products that you can buy in supermarkets. To be connected, two products have to be bought together by the same customers in a significant number of times. What does that mean? By pure intuition, bread and water aren’t going to be connected: both of them are bought very frequently, but they have little to do with each other, thus they are expected to be in the same shopping cart by chance. Eggs and flour are too very popular, but probably more than chance, since there are a lot of things you can do with them together. Therefore they are connected. Other specific pairs of products, say bacon flavoured lipstick and liquorice shoelaces, may ended up in the same, quite weird, shopping cart. But we don’t connect them, as their volume of sales is too low (or at least I hope so).

Here are some of the facts we found. First. The overlapping approach* tends to return relatively more communities with a larger amount of nodes than the partition approach**. In absolute terms that’s obvious, since the same node is counted more than once, but here the key term is “relatively”. See the plot above on the right, where we graph the probability (y axis) of finding a community with a given number of nodes (x axis). Second. The overlapping approach returns more “messy” communities. Our messiness measure checks how many different product categories are grouped together on average in the same community. Again, larger communities are expected to be messier, but the messiness measure that we used controls for community size. See the plot on the right, again the probability (y axis) of finding a community with a given entropy (x axis, “entropy” is the fancy scientific term for “messiness”). Third. The partition approach returned denser communities, whose link strength (the number of people buying the products together) is higher.

What is the meaning of all this? In our opinion, the two algorithms are aiming to do something completely different. The partition approach is aiming to create a new marketing classification. It more or less coincides with the established one (thus lower messiness), most customers buy those products together (high link strength) and there are very few giant categories (most communities are small). The overlapping approach, instead, wants to do customer profiling. A customer rarely buys all products of a marketing category (thus increasing its messiness), it has specific needs (that not many people have, thus lowering edge weight) and she usually needs a bunch of stuff (thus larger communities, on average).

Who’s right? That’s the catch: both. The fact that two results are incompatible, in this case, does not mean that one is right and one is wrong. They are just different applications. Which was exactly what I wanted to prove, in this narrow and very specific, probably unsurprising, scenario. Now you should feel better: I gave you a small proof that the hours you spend to choose the perfect toaster for you are really worth your time!

* As overlapping approach, we used the Hierarchical Link Clustering.

** As partitioning approach, we used Infomap.

Today I am going to commit one of the most hideous crimes in the research community. Today I am going to use my knowledge and expertise in my area to tell people in other areas what is a cool thing to do in their job. And I don’t even have the excuse of my age. Though you may say I was already crazy to begin with. My post is about putting some networky juice in literature studies and humanities. I am not the only one doing that – or to say that the complete segregation between humanities and science should not be there.

I already wrote a post about a network approach to the organization of classical archaeology literature. But maybe because of my computing humanities background, maybe because I always loved studying literature, I want to go deeper. So I reasoned about this a bit with my usual friends back in Italy and what came out is just a crazy thought. What if we try to create the idea for a network-based history of literature? That is to say: can we find in the network structure of pieces of literature art some traces of their meaning, of the relationships between them and their times, of the philosophy that moves them?

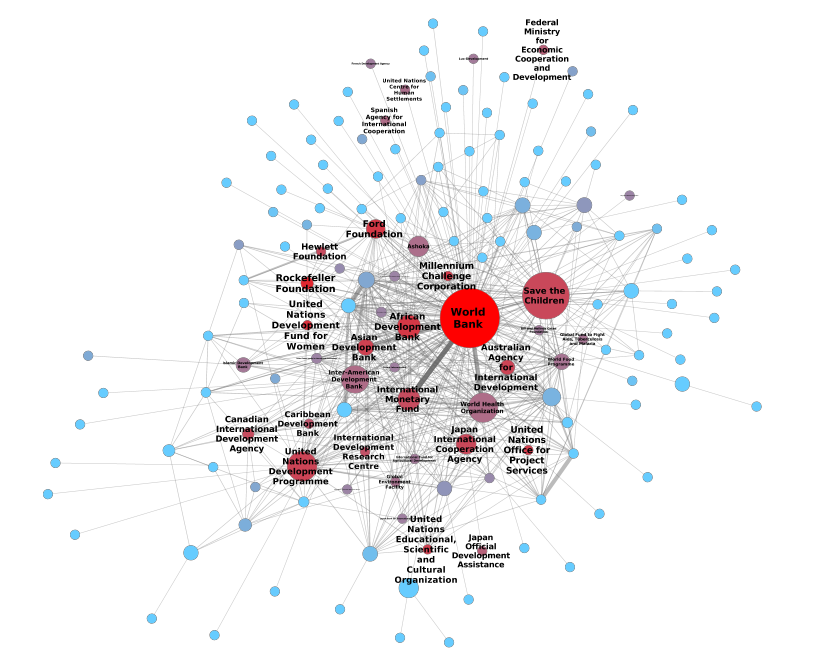
The first product coming out from this crazy idea was “The Social Network of Dante’s Inferno“, presented in the 2010 edition of the “Arts, Humanities and Complex Networks” symposium of NetSci and then published in a 2011 special issue of the Leonardo journal. In this work we were moved by the question: is a network of characters following some particular predictive patterns? If so: which ones?

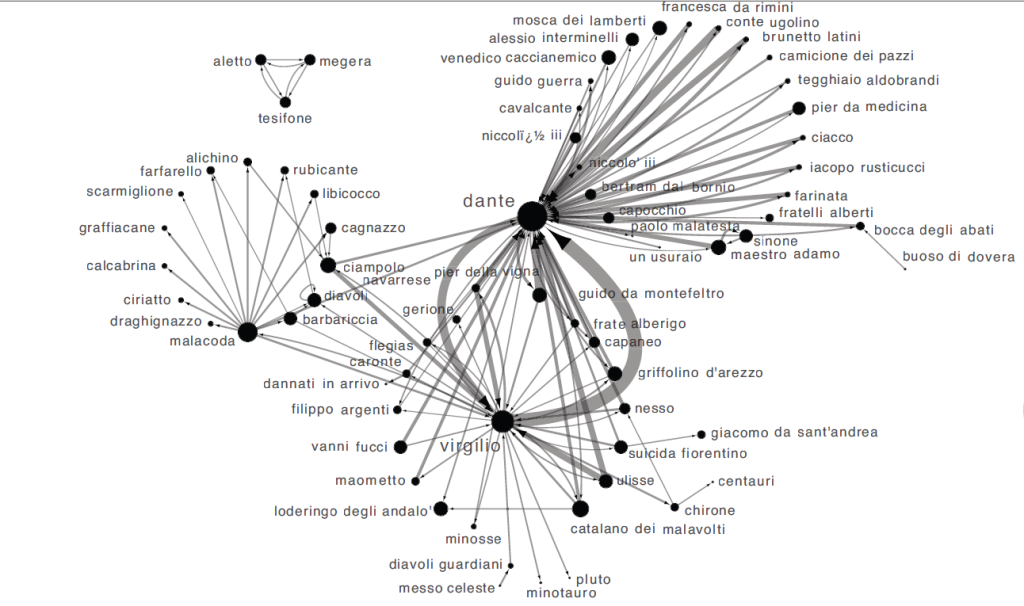
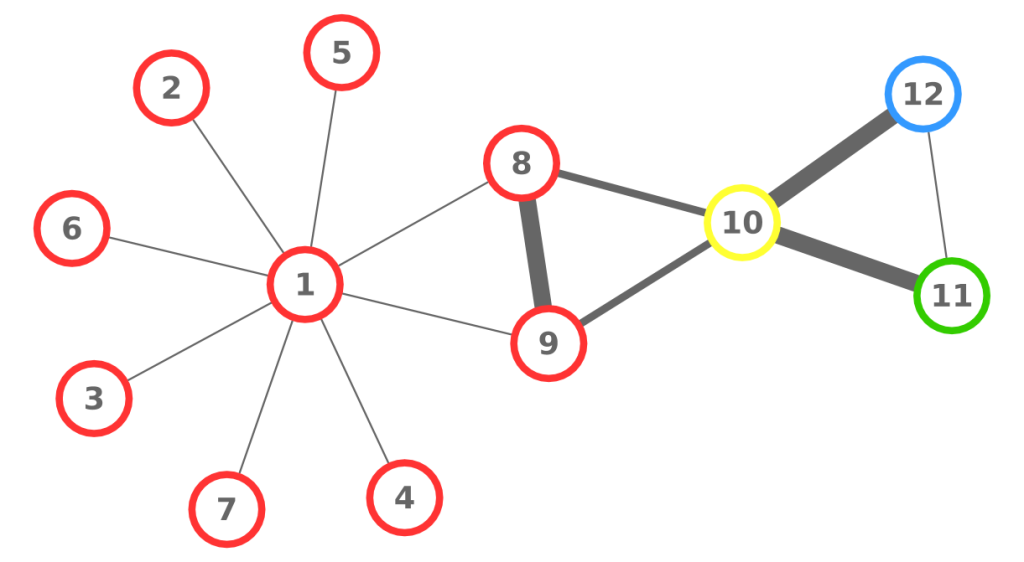
So we took a digital copy of Dante’s Inferno, where all interactions and characters were annotated with extra information (who the character was, if she was a historic or mythological figure, when she lived, …). We then considered each character as a node of the network. We created an edge between two characters if they had at least a direct exchange of words. Normal people would call this “a dialogue”. The result was pretty to see (click for a larger version):

The double-focus point of the Commedia emerges quite naturally, as Dante and Virgilio are the so-called “hubs” of the system. It is a nice textbook example of the rich-get-richer effect, a classic network result. But contrary to what the title of the paper says, we went beyond that. There are not only “social” relationships. Each character is also connected to all the information we have about her. There is another layer, a semantic one, where we have nodes such as “Guelph” or “Middle Ages”. These nodes enable us to browse the Commedia as a network of concepts that Dante wanted to connect in one way or another. One can ask some questions like “are Ghibelline characters preferably connected to historic or mythological characters?” or “what’s the centrality of political characters in the Inferno as opposed to the Purgatorio?” and create one’s own interpretation of the Commedia.

As fun as it was, we wanted to push this idea a bit beyond the simple “put a network there and see what happens”. That’s when Emmanuele Chersoni knocked on my door. He had manually annotated the Orlando Furioso (“The Frenzy of Orlando”) and the Gerusalemme Liberata (“Jerusalem Delivered”), two of the greatest masterpieces of the Italian epic poetry. This time it was the perfect occasion for a legendary artistic stand off.

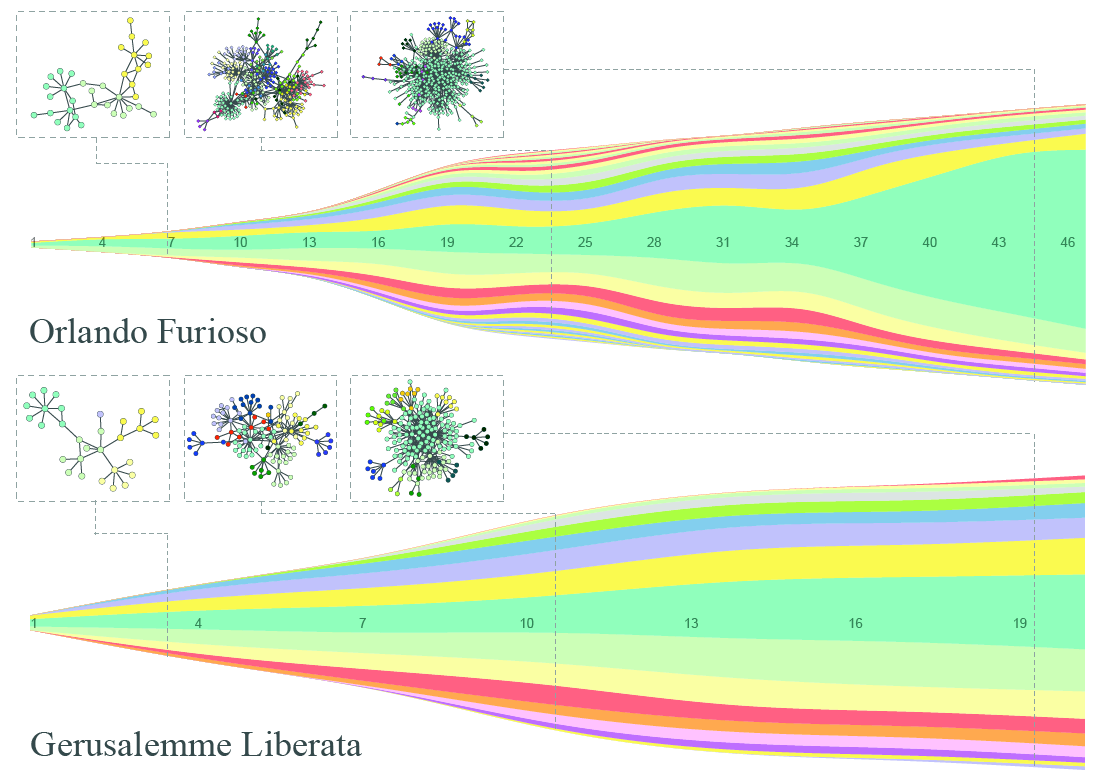
To drive the theory a bit further, we asked ourselves: can we find in the network structure of a poem the principles of the poetics of the time and other factors influencing the authors? We knew that, in the century between the two poems, there was a transformation of the genre and significant historical and sociopolitical changes: a canonization of the genre took place, with more rigorous narrative structures and with the avoidance of the proliferation of plotlines. We wanted to see if these changes in the “rules of the game” could be rediscovered in the final product.

To test the hypothesis, we again created a character-character interaction network. We then grouped together characters with a community discovery algorithm (what else? 🙂 ). If the network is telling us something about the effects of this transformation of the genre, then the Gerusalemme Liberata should grow more organically, without many fluctuating sub-plots and a general collapse in the main plot at the end. And, surprise surprise, that’s exactly what we see. In the visualization below, we have a steamgraph where each color represents a community, its size proportional to the number of characters in it. And to me, the squiggly Orlando Furioso, with the central plot that becomes a giant at the end, seems not regular at all (click to enjoy the full resolution):

To conclude, let’s go back to the initial question. Why are we doing this? Because I feel that there is a fundamental flaw in the history of literature as it was taught to me. Rather than exclusively studying a handful of “significant works” per century, I’d want to also get a more wide knowledge about what were the fundamental characteristics of the art of the period. Network analysis can prove itself useful in this task. It “just” takes the effort of annotating many of these works, and then it can carry on the analysis in an almost automatic way. The result? To know what were the topical structures, theme connections, genre relations (yes, I go much further beyond what I showed, but I’m a dreamer). And how they gradually evolved over time. And who were the real authors who firstly used some topical structures. To me, it’s a lot, a goldmine, a kid-in-a-candy-store avalanche effect.

The four of you who follow this blog regularly will know that I have a thing for something called “community discovery“. That’s because no matter how you call it, it always sounds damn cool. “Discovering Communities” or “Detecting the functional modules” or “Uncovering node clusters”. These are all names given to the task of finding groups of nodes in a network that are very similar to each other. And they make you feel like some kind of wizard. Adding to that, there are countless applications in epidemiology, sociology, immunology, marketing.

Far from being original, I share this passion with at least a thousand researchers. Being as smart as they are, they quickly realized that there are many ways in which you can group nodes based on their similarity. On the one hand, this is good news, as we basically have an algorithm for any possible community you want to find in your network. On the other hand, this made a lot of people freak out, as too many algorithms and too different solutions are usually a big red flag in computer science. A flag that says: “You have no idea what you are doing!” (although a computer scientist would put it in the cold and rational “Your problem is not formally defined”: it means the same).

Yes, my signature “Community Discovery Picture” strikes again!

I personally think that the plus side is more predominant than the minus side, and you can get rid of the latter with a bit of work. Work that I have done with Dino Pedreschi and Fosca Giannotti in our paper “A classification for Community Discovery Methods in Complex Networks“. The trick is very simple. It just consists in noticing what’s wrong with the starting point. “Finding groups of nodes in a network that are very similar to each other”. Exactly what is “similar“? It is an umbrella term that can be interpreted in many different ways. After all, we already do this outside of network science. People can be very similar because they look alike. Or because they like the same things. So why can’t we just have different definitions of communities, based on how we intend similarity?

Well, because at the beginning of community discovery we thought that the problem was well defined. The first definition of community was something like: “A community is a group of nodes that are densely connected, and they have few edges connecting them to nodes outside the community”. Which is fine. In some cases. In others, we discovered that it doesn’t really make sense. For example, we discovered that many social networks have a pervasive overlap. It means that nodes are densely connected with many different groups, disproving the definition: now, the area outside the community could be just as dense as the community itself! And this is just one example: you take a hundred community discovery algorithms in literature and you’ll get a hundred different community results on the same network.

Overlap in the infamous Zachary Karate Club network, you can even win a prize if you mention it!

So now researchers in the community discovery… well… community were divided in three factions. We had those who thought that the problem was ill defined, thus everything done so far was just a royal mess. Then there were those who still thought that the problem was well defined, because their definition of community was the only one standing on solid ground and everybody else was just running around like a headless chicken. And then there were people like me and Sune Lehmann (whom I thank for the useful discussions). Our point was that there were many different definitions of communities, and the incompatible results are just the output of incompatible definitions of community.

This is the main take-away message of the paper. We then moved on and tried to actually spot and categorize all different community definitions (for 90s kids: think of a Pokédex for algorithms). Some choices were easy, some others weren’t. I personally think that more than an established classification, this is just a conversation starter. Also because the boundaries between community definitions are at least as fuzzy as the boundaries between the communities themselves. Algorithms in one category may also satisfy conditions imposed by another category. And to me that’s fine: I don’t really like to put things in separate boxes, I just want to have an insight about them.

I put tags, not classes.

So here you go, the classification we made includes the following “community types” (names are slightly changed from the paper, but it should be obvious which is which):

• Common Features: in this definition, each node has a number of attributes. If we are in a social network and the nodes are people, these attributes may well be the social connections, the movies you like, the songs you listen to. Communities are groups of nodes with similar attributes.
• Internal Density: the classical starting point of community discovery. Here we are interested in just maximizing the number of edges inside the communities.
• External Sparsity: a subtle variant of the Internal Density class. The focus of this definition is on considering communities as islands of nodes, not necessarily densely connected.
• Action Communities: this is a very dynamic definition of communities. Nodes are not just static entities, but they perform actions. Again, in a social network you not only like a particular artist: you listen to her songs. If your listening happens with the same, or similar, dynamics of other people, then you might as well form a community with them.
• Proximal Nodes: here we want the edges inside the communities to make it easy for a node to be connected to all other nodes in the community. Or: to get to any other node in the community I have to follow just a few edges.
• Fixed Structure: this is a very demanding community definition. It says that the algorithm knows what a community looks like and it just has to find that structure in the network.
• Link Communities: one of my favorites, because it revolutionizes the idea of community. Here we think that we need to group the edges, not the nodes. In a social network, we know different people for different reasons: family, work, free time, … The reason why you know somebody is the community. And you belong to many of them: to all the communities your edges belong to.
• Others: in any decent classification there must be a miscellaneous category! Some algorithms do not really follow a particular definition, whether because they just add features to other community discovery algorithms or because they let the user define their communities and then try to find them.

And now just a shortlist of readily available community discovery algorithms you can find on the Web:

• DEMON (by yours truly)
• HLC
• Infomap
• Label Propagation, Walktrap and Modularity Maximization (in the igraph library, either source code in C or for R or Python)
• BigClam (in the SNAP network library)
• k-Clique (in the Networkx Python package)
• CONGA/Peacock
• Edge Clustering
• PMM
• Fast Unfolding Modularity
• Conclude

That’s it! I hope I created a couple of new community discovery aficionados!

“It’s a bit sad that some among the most brilliant minds of our generation are working tirelessly on strategies to increase clicks on online ads” popped up on my Facebook stream some days ago (I don’t remember who wrote it, so you are welcome to contact me to restore credit where credit is due 🙂 ). But the point still remains. I actually don’t find it that bad. Yes, it’s bad, but it could be worse. It reminds me of other “wrong” reasons to do incredible improvements in science and stuff. For example, war is responsible for many technology advancements. Even if the aim of online marketing is just to increase revenues, what it actually requires is to understand human psychology, behavior and social interactions. In practice, that’s philosophy of the human mind at its best: how does the brain work? How does a collection of brains work? What drives our behavior and needs?

When you put together many minds in the real world, you have to deal with complex networks. We are not connected with one another at random, and the eyes of our friends are the channel through which we observe the world. This fact is studied in complex network analysis, in the sub-branch of cascade behaviors. Cascade behaviors happen when a person in a social network decides to modify her behavior according to the behavior of the people she is connected to. As a consequence, there are some people in the network who are in a very particular position: given the people they know and their prominence among them, they can modify their behavior and they will modify their friends’ behavior and so on an so forth, changing forever how every node in the network behaves. And that’s the cascade. If you find a way to identify these prominent actors in the network, you can control the behavior of the entire system. Now you can see why there is a mountain of work about it. In the computer science approach, we have threshold models simulating the cascade for many starting nodes and thus identify the practical leaders (for example Jon Kleinberg’s work); in physics we have models, aiming at understanding the degree of controllability of complex systems (I’ll go with Laszlo Barabasi in this).

Visualization of network cascade, from my good friend Mauro Martino. The red dots at the bottom are the “drivers”, who influence the collection of green nodes they are attached to.

Genuinely curious about the topic, I started my own track of research on it. One thing that Diego Pennacchioli, Giulio Rossetti, Luca Pappalardo, Dino Pedreschi, Fosca Giannotti and me found curious is that everybody working on social prominence was looking at it from a monodimensional perspective. That means: the only thing they are interested in is how to maximize the number of nodes influenced by the leaders. The bigger this number, the better. All fun and games, but why? I can think about several scenarios where the final total number is not the most important thing. For example:

• What if I want people to buy a product? The total number of people knowing about the product is nice, but I want them to be strongly committed, strongly enough to buy it.
• What if I am actually looking to reach a particular person? Then I care how deeply my message can go through the network.
• What if I just care about my friends? Then screw their friends (and everybody else), as long as I can influence a wide range of my direct connections!

To calculate our measure we need to infer the diffusion trees. So from the left, where the number on each arrow gives you the action time of the node at the base of the arrow, we go to the right by selecting the lowest possible combination of arrows.

Strength, depth and width of social prominence. That’s why our paper is called “The Three Dimensions of Social Prominence” (check it out). Strength is how committed the people you influenced are to keep doing what you influenced them to do. Depth is how many degrees of separation (or, how far) the cascade of influence that you triggered can go. Width is simply the ratio of your friends that you are able to influence. By analyzing how much a user in Last.fm (a social website based on music) is able to influence her friends in listening to new artists, we found a collection of very interesting facts.

For example, it is well known that in social networks there are some nodes that are structurally very important. They are the central users, the ones that keep the network connected. Intuitively, they are the only way, or the easiest way, through which a signal (in our case social influence) can go from one part of the network to the other. Guess what: they can’t do it. We found a significant anti-correlation between centrality and width and depth. That is bad news, because those nodes are the ones in the only position with a theoretical ability of controlling the network and a practical inability in doing so. I like to call it “The Paradox of Social Controllability” (hence, the post title).

The anti-correlation between depth and strength.

Another piece of food for thought is the trade off between strength and depth. While width is unrelated to both, we found that if you want to go deeply into the network, then you can’t expect that the people you touch will be extremely committed to your message.

The third big thing is the distribution of connections per leader. We found that the leaders showing highest values of strength, depth and width were those who used Last.fm with average frequency. The highly connected and very active users (hubs, in network lingo) scored poorly, as we saw. So did the occasional users, the ones with just two or three connections (that is the majority of the system). The people who have control over the network are the mildly engaged. They are you, in practice: chances are that you are not a record label, nor a music fanatic, but just a person with her tastes and preferences. So you have control. Problem is, the control is scattered equally on the vast set of people like you.

To conclude, we saw what wonderful things network cascades are: they could empower us to do a lot of good. We also saw how there are theoretical results about the possibility of identifying people who can trigger them. But my unfortunate conclusion is about the paradox between theory and practice. Those who theoretically should, apparently can’t.

The Holy Grail of every marketing system is to understand how the mind of the customers works. For example answering the question: “From how far can I attract customers?” To do so means to increase profits. You can deploy your communication and products more efficiently and maximize your returns. Clearly, there is no silver bullet for this task. There is no way that one single aspect is so predominant in a person’s mind at the point of empowering a seller to have perfect control over who will buy her product, where and when. If that would be true, there would be no space left for marketing specialists, demand segmentation and so on. Many little tricks can be deployed in the market.

I am by no means an expert on the field, so my way to frame this problem may sound trivial. In any case, I can list three obvious parameters that affect a customer’s decision in buying or not buying a product. The first is price. Few people want to throw their money senselessly, most of them want to literally maximize the bang for their buck (okay, maybe not that literally). The second is the quantities needed: if I need to buy product X everyday in large bulks and product Y once in a blue moon, then it’s only fair to assume that I’ll consider different parameters to evaluate X and Y.

The third is the level of sophistication of a given product. There are things that fewer and fewer people need: birdseed, piña colada flavored lip balm. Narrower customer base means less widespread offer, thus the need of travel more to specialized shops. Intuitively, sophistication is more powerful than price and quantity: a Lamborghini is still a car – also quite useless when doing groceries – like a Panda, but it satisfies very different and much more sophisticated needs. Sophistication is powerful because you can play with it, increasing the perceived sophistication of a product, thus your market: like Jonah Berger‘s  “thee types of ice” bar, that looked more fancy just by inventing a way to make ice sound more sophisticated than it is.

So let’s play and try to use these concepts operatively. Say we want to predict the distance a customer is willing to travel to buy a product. Then, we try to predict such a distance using different variables. The one leading to better predictions of these distances wins as the best variable describing what motivates a customer to travel. We decided to test the three variables I presented before: price, quantity and sophistication. In this theory, higher prices mean longer distances to travel, as if I have to buy an expensive TV I’ll probably go around and check where is the best quality-price ratio. Higher quantities mean shorter distances, as if I have to buy bread everyday I don’t care where the best bakery of the city is if that means traveling ten kilometers everyday. Finally, higher sophistication means longer distances: if I have sophisticated needs I need to travel a lot to satisfy them.

Price and quantity are easy to deal with: they are just numbers. So we can put them on the X axis of a plot and put the distance traveled on the Y axis. And that’s what we did, for price:

and for quantity:

Here, each dot is a customer buying a product. If the dots had the same distance and the same price/quantity then we merged them together (brighter color = more dots here). We see that our theory, while not perfect, is correct: higher prices means longer distances traveled, higher quantities means shorter distances. Time to test for the level of sophistication! But now we hit a brick wall. How on earth am I suppose to measure the level of sophistication of a person and of a product? Should I split the brain of that person in half? How can I do this for thousands or millions of customers? We need to invent a brain splitting machine.

That’s more or less what we did. In a joint work with Diego Pennacchioli, Salvo Rinzivillo, Fosca Giannotti and Dino Pedreschi, that will appear in the BigData 2013 conference (you can download the paper, if you are interested), we proposed such a brain slice device. Of course I am somewhat scared by all the blood that would result in literally cutting open thousands of skulls, so we implemented a data mining machine that just quantifies with a number the level of sophistication of a customer’s needs and the level of sophistication that a product can satisfy, solving the issue at hand with no bloodshed.

The fundamental question is: is the level of sophistication a number? Intuition would tell us “no”: it’s a complex multidimensional space and my needs are unique like a snowflake. Kind of. But with a satisfying level of approximation, surprisingly, we can describe sophistication with a number. How is that possible? A couple of facts we discovered: customers buying the least sold products also buy everything else (the “simpler” stuff), and products bought just by few customers are bought only by those who also buy everything else. In other words, if you draw a matrix connecting the customers with the products they buy, this matrix is nested, meaning that all purchases are in the top left corner:

A-ha! Then it’s fair to make this assumption: customers are adding an extra product bought only if they already buy (almost) everything else “before” it. This implies two things: first, is that they add the extra product if all their previous products already satisfied their more basic needs (then, they are more sophisticated); second, is that they are moving on a monodimensional space, adding stuff incrementally. Then, they can be quantified by a number! I won’t go in the boring details about how to calculate this number. Suffice to say that they are very similar to how you calculate a country’s complexity, about which I wrote months ago; and that this number is not the total amount of money they spend, nor the quantity of products they buy.

So, how does this number relate to the distance traveled by customers?

The words you are looking for is “astonishingly well”.

So our quantification of the sophistication level has a number of practical applications. In the paper we explore the task of predicting in which shop a customers will go to buy a given product. We are not claiming that this is the only important factor. But it gives a nice boost. Over a base accuracy of around 53%, using the price or the quantity gives you a +6-7% accuracy. Adding the sophistication level gives an additional +6-8% accuracy (plots would suggest more, but they are about continuous numbers, while in reality shop position is fixed and therefore a mistake of a few hundreds meters is less important). Not bad!

Today I want to talk about jobs. Or, better, about finding a job. Sooner or later, this is a task that many people will have to perform and it is not usually a very enjoyable one. Writing a CV is mostly painful. You have to list all your skills, all the knowledge you have, what you have done in the past, the tasks you can perform. Everything to maximize your value to the eyes of the examiner, who is judge, jury and executioner of your working fate. But, after all, you can’t complain. You know the rules of the game. It is only fair, because the recruiter wants to see the best possible CV and the best possible CV is the one that includes the most relevant information: you have to stuff the maximum amount of skills in your body to maximize your value and it is the most valuable person the one who is going to be picked. Right?

Wrong. There’s one critical flaw to that reasoning, and that is time. Time is limited. You can’t spend too much time in stuffing knowledge into you, because there is too much knowledge out there and if you try to internalize everything you don’t have time to produce anything. This is not just my opinion. It is one of the cornerstones of widely accepted and useful theories, for example the division of labour. This is linked to the concept of “social knowledge“. Social knowledge is the collection of what people in society know. While personal knowledge is bounded by time, social knowledge is not, because many different brains work on it at the same time, making it grow beyond what any individual can grasp.

If you want to have 100 people to make cars, you don’t teach each one of them to make a car from scratch and then you watch them making 100 cars at the same time. Each guy will assemble one part. And he’ll be awesome at that particular part. This applies not only to manufacturing. How many times in your working life you found yourself struck with a problem, not exactly in your knowledge domain, and you solved it by simply asking someone about it? In my case, many. Think about how many times you Google something. That’s accessing the social knowledge of humanity. That is one of the reasons why, for example, the social return of education exceeds the private return.

The way you access social knowledge also changes the usefulness of it. It is better if a friend takes time to explain things to you than if you have to read an answer in Quora, that is also related only to some extent to your specific problem. Because tacit knowledge needs a broker to make it explicit and understandable. So it is better to have knowledgeable friends in many fields, or: your social network matters for your qualifications, because it’s the principal medium you use to get explicit knowledge from the tacit social knowledge.

So it seems like we are onto an interesting problem. On one hand, I hope to have convinced you that social knowledge is an important component of someone’s value; on the other hand that creates more questions than answers. How do we evaluate a person for a job? How do we measure the social knowledge she has access to? Well, if you know me you know what’s going to happen. A network algorithm, of course! Precisely, an algorithm with a flavor of Philip K. Dick in its name: UBIK, or “U know Because I Know”. This algorithm has been created and developed with the help of Giulio Rossetti, Diego Pennacchioli and Damiano Ceccarelli and has resulted in a paper published in the ASONAM 2013 conference that will take place later this month. Also, the code of UBIK is available for use.

Here’s how UBIK works. First, you have to start by collecting information about the social connections of people. It’s even better if you can find multiple types of connections from multiple sources, because the channel through which knowledge passes influences the quality of that knowledge. Second, for each person you have to collect their CV. Personal knowledge is still important. Once you have these pieces of information, UBIK can unweave its magic.

Let’s look at a simple example. The above picture can be considered a network of people: each node is a person, each person is connected to the people she knows, her color represents the skill in which she is specialized, and the width of the link is the strength of the connection (important: UBIK works with qualities of links, not strengths, but for the sake of simplicity in this example we use the latter). The consequence of our theory is that the skills of each person are transferred through the links of the network. Also, a direct connection is stronger than a connection through another node. For example, node 8 passes her skills more efficiently to 1 than node 10 does.

So, at the first iteration, UBIK passes the skills of each node to its neighbors. Node 1 gets a lot of red skill, node 10 gets all kinds of skills. It is a percolation process. At each iteration, UBIK keeps passing the entire set of updated skills, with an increasing penalty due to the social distance. I won’t bother you with the equations. Just know that, at some point, the penalty is so high that the algorithm stops.  The skill transfer happens proportionally to the strength of the links connecting the nodes. As a result, node 10 is super valuable, because she has access to the knowledge about all skills in the network, while for example node 1 will be a uber-specialist of the red skill. By just looking at their CV, it would be impossible to extract this information.

Some of you familiar with network analysis may have some bells ringing in their heads. “This is node ranking!” Well, yes. “So just use PageRank!” “Or HITS!” “Why do we need UBIK?” Well, for a number of reasons. First, UBIK handles multiple link types and multiple skills at the same time: (variants of) PageRank and HITS can do one or the other, but not so many can do it simultaneously yielding effective results. Second, PageRank and HITS have flaws. PageRank correlates with degree (the number of connections of a node) and centrality measures: see the above picture where we confront the rankings of the algorithms with the degree rank. HITS has similar flaws related to the nodes’ tendency of cluster in communities.

Moreover, when we applied the algorithms to network of researchers, UBIK was most likely to rank them in the same way as measures independent from networks such as the H-Index. This shows that UBIK may be more useful than other network ranking techniques when these independent evaluation criteria are not available. The beauty of UBIK consists in multiple rankings. Below I report some rankings of researchers in Computer Science. Each number is the rank that UBIK gave to the researcher in a particular conference. Each conference is a different ranking that UBIK is able to distinguish. We are able to spot the specialists of many computer science conferences, highlighting their prominence in one community and low ranking in others. Also, we report the rankings in these conferences for the most prominent general authors, showing that they rank on average well in many different venues, but they are not really specialists.

And that’s why you should give UBIK a chance.

The second half of the year, for me, is conference time. This year is no exception and, after enjoying NetSci in June, this month I went to ICWSM: International Conference on Weblogs and Social Media. Those who think little of me (not many, just because nobody knows me) would say that I went there just because it was organized close to home. It’s the first conference for which I travel not via plane, but via bike (and lovin’ it). But those people are just haters: I was there because I had a glorious paper, the one about internet memes I wrote about a couple of months ago.

In any case, let’s try to not be so self-centered now (good joke to read in a personal website, with my name in the URL, talking about my work). The first awesome thing coming to my mind are the two very good keynotes. The first one, by David Lazer, was about bridging the gap between social scientists and computer scientists, which is one of the aims of the conference itself. Actually, I have been overwhelmed by the amount of the good work presented by David, not being able to properly digest the message. I was struck with awe by the ability of his team to get great insights from any source of data about politics and society (one among the great works was about who and how people contact other people after a shock, like the recent Boston bombings).

For the second keynote, the names speak for themselves: Fernanda Viégas and Martin Wattenberg. They are the creators of ManyEyes, an awesome website where you can upload your data, in almost any form, and visualize it with many easy-to-use tools. They constantly do a great job in infographics, data visualization and scientific design. They had a very easy time pleasing the audience with examples of their works: from the older visualizations of Wikipedia activities to the more recent wind maps that I am including below because they are just mesmerizing (they are also on the cover of an awesome book about data visualization by Isabel Meirelles). Talks like this are the best way to convince you of the importance of a good communication in every aspect of your work, whether it is scientific or not.

As you know, I was there to present my work about internet memes, trying to prove that they indeed are proper memes and they are characterized by competition, collaboration, high-order organization and, maybe I’ll be able to prove in the future, mutation and evolution. I knew I was not alone in this and I had the pleasure to meet Christian Bauckhage, who shares with me an interest in the subject and a scientific approach to it. His presentation was a follow-up to his 2011 paper and provides even more insights about how we can model the life-span of an internet meme. Too bad we are up against a very influential person, who recently stated his skepticism about internet memes. Or maybe he didn’t, as the second half of his talk seems to contradict part of the first, and his message goes a bit deeper:

http://www.youtube.com/watch?v=GFn-ixX9edg

Other great works from the first day include a great insight about how families relate to each other on Facebook, from Adamic’s group. Alice Marwick also treated us to a sociological dive into the world of fashion bloggers, in the search of the value and the meaning of authenticity in this community. But I have to say that my personal award for the best presentation of the conference goes to “The Secret Life of Online Moms” by Sarita Yardi Schoenebeck. It is a hilarious exploration of YouBeMom, a discussion platform where moms can discuss with each other preserving their complete anonymity. It is basically a 4chan for moms. For those who know 4chan, I mean that literally. For those who don’t, you can do on of two things to understand it: taking a look or just watching this extract from 30 Rock, that is even too vanilla in representing the reality:

I also really liked the statistical study about emoticon usage in Twitter across different cultures, by Meeyoung Cha‘s team. Apparently, horizontal emoticons with a mouth, like “:)”, are very Western, while vertical emoticons without a mouth are very Eastern (like “.\/.”, one of my personal favorites, seen in a South Korean movie). Is it possible that this is a cultural trait due to different face recognition routines of Western and Eastern people? Sadly, the Western emoticon variation that includes a nose “:-)”, and that I particularly like to use, apparently is correlated with age. I’m an old person thrown in a world where young people are so impatient that they can’t lose time pressing a single key to give a nose to their emoticons :–(

My other personal honorable mention goes to Morstatter et al.’s work. These guys had the privilege to access the Twitter Firehouse APIs, granting them the possibility of analyzing the entire Twitter stream. After that, they crawled Twitter using also the free public APIs, which give access to 1% of all Twitter streams. They shown that the sampling of this 1% is not random, is not representative, is not anything. Therefore, all studies that involve data gathering through the public APIs have to focus on phenomena that include less than 1% of the tweets (because in that case even the public APIs return all results), otherwise the results are doomed to be greatly biased.

Workshops and tutorials, held after the conference, were very interesting too. Particularly one, I have to say: Multiple Network Models. Sounds familiar? That would be because it is the tutorial version of the satellite I did with Matteo Magnani. Luca Rossi and others at NetSci. Uooops! This time I am not to blame, I swear! Matteo and Luca organized the thing all by themselves and they did a great job in explaining details about how to deal with these monstrous multiple networks, just like I did in an older post here.

I think this sums up pretty much my best-of-the-best picks from a very interesting conference. Looking forward to trying to be there also next year!

As I mentioned a couple of months ago, during the first week of June the NetSci conference took place. NetSci is the main venue that brings together all researchers interested and involved in network science. It has always been a gigantic opportunity to put you in contact with the big shots in network analysis and an excellent playground for very interesting discussions. This year was no different.

Of course, for me the most important part of it was the very first day, when the satellite on multiple networks (organized by myself together with Matteo Magnani, Dino Pedreschi, Luca Rossi, Guido Caldarelli and Przemyslaw Kazienko) happened. As I wrote more than once in the past, multiple networks are networks in which the nodes may be connected with different kinds of interactions (friendship, collaboration, and so on).

It was an extremely interesting event; a first step to bring together many researchers working on the topic of multiple networks, most of whom hadn’t spoken to each other up until then. And when I say it was a smooth and successful operation, you don’t have to take my word for it. We have proof of a room full of brilliant minds taking up all the available spots… and beyond:

The talks were very impressive:

• We learnt how to measure eigenvector centrality on multiple networks (and you can too);
• We learnt how to extend basic measures from regular complex networks to multiple networks (and you can too);
• We learnt how to mine network with heterogeneous information on nodes and edges (and you can too);
• We learnt how to detect communities on multiple networks (and you can too);
• We learnt how to infer the latent structure of inter-related networks (and you can too);
• We learnt how a random walker behaves on dynamic networks (and you can too);
• We learnt about the structure and dynamics of multiple networks (and you can too);
• And we learnt how the properties of multiple networks arise when adding one network at a time (and you can too).

But NetSci, of course, was much more than just this satellite. Another event you absolutely didn’t want to miss there was the Arts, Humanities and Complex Networks Symposium, organized by Max Schich and Isabel Meirelles.

They are both great guys, with a gigantic knowledge about art and design. For example, they picked up a great reference for the logo of their symposium, namely one of the most known infographics made about visual arts, by Alfred Barr:

And besides the usual great lineup of talks (from the Wikidata project to a very cool movie ranking multiple network algorithm) you can learn surprising stuff about basically everything. My favorite: the observation of one of the speakers about the above visualization itself. Apparently, he was the first to realize that there is a bull up there (hint: Cubism lays in between the bull’s horns). As Max then puts it:

Then… the rest of the conference. It is impossible to even give a close idea of the overload of ideas and flashes of genius that populated the venue for those three days. I’ll work around the problem and cheat by giving you a laundry list of (a very tight subset of) the things that most impressed me during the conference:

• The excellent invited talk by Shlomo Havlin about interdependent networks (networks which depend on each other to function, much like a computer network controlling the electric grid). This interests me because he claims that interdependent networks are a more general case of multiple networks (although I personally have an inkling that perhaps they can be reduced to the same model);
• The usual spectacular presentation style of my friend Cesàr Hidalgo, who this time talked about a complex system showing a nested structure: namely, the cultural exports of different countries;
• A really great contributed talk by Esteban Moro, which in my opinion could have been a keynote speech as well. Dr. Moro highlighted how people have a trade-off between social capacity (how many relationships we can keep alive) and social activity (how many new people we can meet). As a consequence, different social strategies arise;
• A brilliant mathematical formulation of a network problem by Jure Leskovec, that, in my opinion, could be the final word about the problem itself. And it resembles the formal mathematical formulation of the same algorithmic idea behind my DEMON;
• And the hilarious ignite talks, 5 minutes and 20 slides for each speaker. There was no possibility of interacting, with the presentation automatically jumping to the next slide every 15 seconds. Next year I definitely want to try to do one too.

And, of course, many other things. But you get the idea: blog posts about it are boring, you really have to experience it yourself.